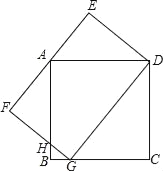
【题目】如图，G是边长为4的正方形ABCD的边BC上的一点，矩形DEFG的边EF过A，GD=5．
（1）指出图中所有的相似三角形；
（2）求FG的长．
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AB=AD，AC与BD交于点E，∠ADB=∠ACB．
（1）求证：
；
（2）若AB⊥AC，AE：EC=1：2，F是BC中点，求证：四边形ABFD是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
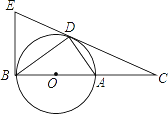
（1）求证：CD是⊙O的切线．
（2）过点B作⊙O的切线交CD的延长线于点E，若OB=5，BC=18，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
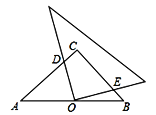
【题目】如图，在等腰直角
中， 
，点
是
的中点，且AC=3，将一块直角三角板的直角顶点放在点处，始终保持该直角三角板的两直角边分别与
、
相交，交点分别为
、
，则
___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
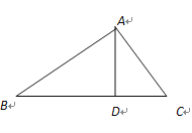
【题目】如图，△ABC中，∠BAC=90°，AD⊥BC，垂足为D．
(1)求作∠ABC的平分线，分别交AD，AC于E，F两点；(要求：尺规作图，保留作图痕迹，不写作法)
(2)证明：AE=AF．
查看答案和解析>>
科目：初中数学 来源： 题型：
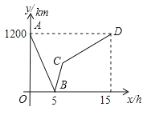
【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，慢车的速度是快车速度的
，两车同时出发．设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．
根据图象解决以下问题：
（1）甲、乙两地之间的距离为 km；D点的坐标为 ；
（2）求线段BC的函数关系式，并写出自变量x的取值范围；
（3）若第二列快车从乙地出发驶往甲地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车追上慢车．求第二列快车比第一列快车晚出发多少小时？
查看答案和解析>>
科目：初中数学 来源： 题型：
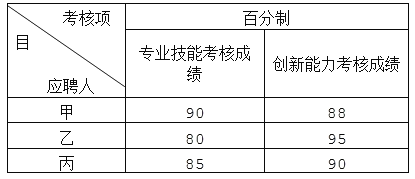
【题目】某广告公司为了招聘一名创意策划，准备从专业技能和创新能力两方面进行考核，成绩高者录取．甲、乙、丙三名应聘者的考核成绩以百分制统计如下：
（1）如果公司认为专业技能和创新能力同等重要，则应聘人 将被录取．
（2）如果公司认为职员的创新能力比专业技能重要，因此分别赋予它们6和4的权．计算他们赋权后各自的平均成绩，并说明谁将被录取．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
和
都是等腰直角三角形，
．
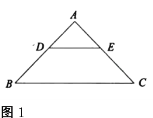
（1）如图1，点
、
分别在
、
上，则
、
满足怎样的数量关系和位置关系？（直接写出答案）
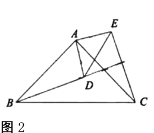
（2）如图2，点在内部，点在外部，连结、，则、满足怎样的数量关系和位置关系？请说明理由．
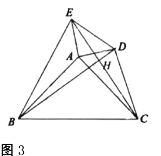
（3）如图3，点、都在外部，连结、、
、
，与相交于
点．已知
，
，设
，
，求
与
之间的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，解答问题．
例：用图象法解一元二次不等式：x2﹣2x﹣3＞0
解：设y=x2﹣2x﹣3，则y是x的二次函数．∵a=1＞0，∴抛物线开口向上．
又∵当y=0时，x2﹣2x﹣3=0，解得x1=﹣1，x2=3．
∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示．
观察函数图象可知：当x＜﹣1或x＞3时，y＞0．
∴x2﹣2x﹣3＞0的解集是：x＜﹣1或x＞3．
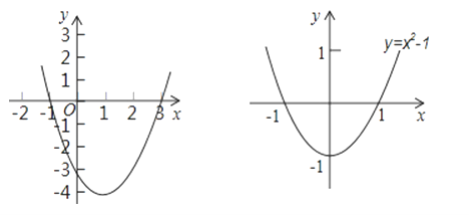
（1）观察图象，直接写出一元二次不等式：x2﹣2x﹣3＞0的解集是 ________；
（2）仿照上例，用图象法解一元二次不等式：x2﹣1＞0．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
