
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
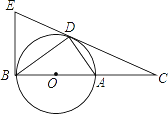
(1)求证:CD是⊙O的切线.
(2)过点B作⊙O的切线交CD的延长线于点E,若OB=5,BC=18,求BE的长.
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)连接OD,根据AB所对的角是直角,以及等边对等角,证明∠ODC=90°,则可以证得;
(2)在直角△ODC中利用勾股定理求得CD的长,然后根据△ABC∽△ODC,利用相似三角形的对应边相等即可求解.
(1)证明:连接OD.
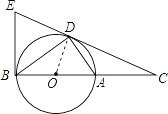
∵AB是直径,
∴∠BDA=90°,
∴∠ABD+∠BAD=90°,
∵OD=OA,
∴∠ODA=∠OAD,
又∵∠CDA=∠CBD,
∴∠CDA+∠ODA=90°,即∠ODC=90°,
∴OD⊥CD,
∴CD是⊙O的切线,
(2)OC=BC﹣OB=18﹣5=13,
直角△OCD中,OD=OB=5,
CD=![]() ,
,
∵BE是圆的切线,
∴∠EBC=90°,
同理∠ODC=90°,
∴∠EBC=∠ODC,
又∵∠C=∠C,
∴△EBC∽△ODC,
∴![]() ,即
,即![]() ,
,
解得:BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与
的图像与![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,且点
,且点![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]() 的值与
的值与![]() 的长;
的长;
(2)若点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某隧道建设工程中,需沿![]() 方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点
方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点![]() 在直线
在直线![]() 上,现在
上,现在![]() 上取一点
上取一点![]() ,
,![]() 外取一点
外取一点![]() ,测得
,测得![]() ,
,![]() ,
,![]() .求开挖点
.求开挖点![]() 到点
到点![]() 的距离.
的距离.
(精确到![]() 米)参考数据:
米)参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
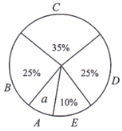
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.等腰三角形的中线与高线重合
C.三边长为![]() 的三角形为直角三角形
的三角形为直角三角形
D.到线段两端距离相等的点在这条线段的垂直平分线上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com