
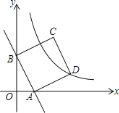
【题目】如图,在平的直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,四边形
,四边形![]() 是正方形,曲线
是正方形,曲线![]() 在第一象限经过点
在第一象限经过点![]() .求双曲线表示的函数解析式.
.求双曲线表示的函数解析式.
【答案】![]() .
.
【解析】
过点D作DE⊥x轴于点E,先由直线y=﹣2x+2与x轴,y轴相交于点A、B求出OB及OA的长,再由全等三角形的判定定理得出△AOB≌△DEA,故可得出D点坐标,再由待定系数法即可求出反比例函数的解析式.
过点D作DE⊥x轴于点E.
∵直线y=﹣2x+2与x轴,y轴相交于点A、B,∴当x=0时,y=2,即OB=2;当y=0时,x=1,即OA=1.
∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠BAO+∠DAE=90°.
∵∠ADE+∠DAE=90°,∴∠BAO=∠ADE.
∵∠AOB=∠DEA=90°,∴△AOB≌△DEA,∴DE=AO=1,AE=BO=2,∴OE=3,DE=1,∴点D的坐标为(3,1)把(3,1)代入y=![]() 中,得:k=3,故反比例函数的解析式为:y=
中,得:k=3,故反比例函数的解析式为:y=![]() .
.


科目:初中数学 来源: 题型:
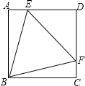
【题目】如图,正方形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() 为等边三角形,下列结论:
为等边三角形,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中正确的结论个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
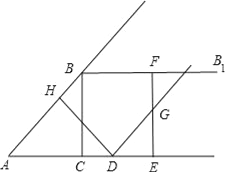
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
(1)求证:![]() ;
;
(2)若AB⊥AC,AE:EC=1:2,F是BC中点,求证:四边形ABFD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
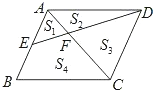
【题目】如图,已知平行四边形ABCD中,E是AB边的中点,DE交AC于点F,AC、DE把它分成的四部分的面积分别为S1S2S3S4,下面结论:
①只有一对相似三角形
②EF:ED=1:2
③S1:S2:S3:S4=1:2:4:5
其中正确的结论是( )
A.①③ B.③ C.① D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日-23日,首届世界![]() 大会在北京举行.某校的学生开展对于
大会在北京举行.某校的学生开展对于![]() 知晓情况的问卷调查,问卷调查的结果分为
知晓情况的问卷调查,问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
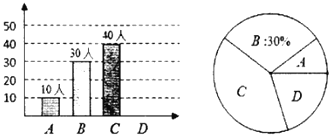
根据上述信息,解答下列问题:
(1)这次一共调查了多少人;
(2)求“![]() 类”在扇形统计图中所占圆心角的度数;
类”在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
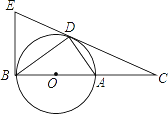
(1)求证:CD是⊙O的切线.
(2)过点B作⊙O的切线交CD的延长线于点E,若OB=5,BC=18,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
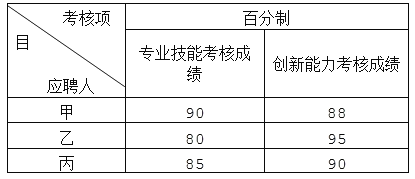
【题目】某广告公司为了招聘一名创意策划,准备从专业技能和创新能力两方面进行考核,成绩高者录取.甲、乙、丙三名应聘者的考核成绩以百分制统计如下:
(1)如果公司认为专业技能和创新能力同等重要,则应聘人 将被录取.
(2)如果公司认为职员的创新能力比专业技能重要,因此分别赋予它们6和4的权.计算他们赋权后各自的平均成绩,并说明谁将被录取.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com