
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=3��BC=4������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F��G��EF�е㣬����DG�����D�˶���ʱ��Ϊt�룮
��1����tΪ��ֵʱ��AD=AB���������ʱDE�ij��ȣ�
��2������DEG���ACB����ʱ����t��ֵ��
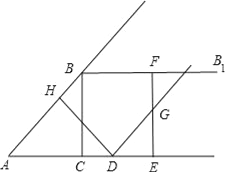
���𰸡���1����t=1ʱ��AD=AB��AE=1��
��2����t=![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ʱ����DEG����ACB����.
ʱ����DEG����ACB����.
�������������������1�����ݹ��ɶ����ó�AB=5,ҪʹAD=AB=5��������Dÿ��5����λ���ٶ��˶�����t=1����2������DEG����ACB����ʱ��Ҫ������������ۣ��������������ε����ʣ��г�����ʽ�����DE�ı���ʽʱ��Ҫ��AD��AE��AD��AE�����������.
���������
��1���ߡ�ACB=90�㣬AC=3��BC=4�� ��AB=![]() =5��
=5��
��AD=5t��CE=3t�� ����AD=ABʱ��5t=5����t=1��
��AE=AC+CE=3+3t=6��DE=6��5=1��
��2����EF=BC=4��G��EF���е㣬 ��GE=2��
��AD��AE����t��![]() ��ʱ��DE=AE��AD=3+3t��5t=3��2t��
��ʱ��DE=AE��AD=3+3t��5t=3��2t��
����DEG����ACB���ƣ��� ![]() ��
�� ![]() ��
��
��![]() ��
��![]() �� ��t=
�� ��t=![]() ��t=
��t=![]() ��
��
��AD��AE����t��![]() ��ʱ��DE=AD��AE=5t����3+3t��=2t��3��
��ʱ��DE=AD��AE=5t����3+3t��=2t��3��
����DEG����ACB���ƣ��� ![]() ��
�� ![]() �� ��
�� ��![]() ��
��![]() ��
��
���t=![]() ��t=
��t=![]() ��
��
������������t=![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ʱ����DEG����ACB���ƣ�
ʱ����DEG����ACB���ƣ�


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
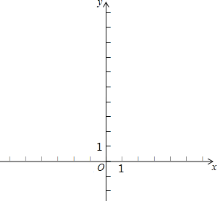
����Ŀ����ƽ��ֱ������ϵ![]() �У���ͼ������֪������
�У���ͼ������֪������![]() ����
����![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
![]() ��������ߵı��﷽ʽ����
��������ߵı��﷽ʽ����![]() �����ꣻ
�����ꣻ
![]() ��
��![]() ����õ���������
����õ���������![]() ������ƽ��
������ƽ��![]() ����λ����������������
����λ����������������![]() ��Ľ����Ϊ��
��Ľ����Ϊ��![]() ����
����![]() ʱ����������ʱ�����
ʱ����������ʱ�����![]() �����ꣻ
�����ꣻ
![]() ����
����![]() ��
��![]() ����õ������ߵĶԳ����ϣ�����
����õ������ߵĶԳ����ϣ�����![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת
��ʱ��ת![]() �õ��߶�
�õ��߶�![]() ������
������![]() ǡ������
ǡ������![]() ����õ��������ϣ����
����õ��������ϣ����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
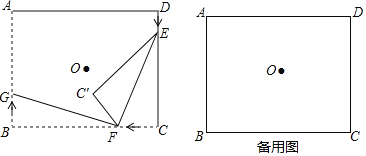
����Ŀ����ͼ����OΪ����ABCD�Խ��߽��㣬![]() ��
��![]() ����E��F��G�ֱ��D��C��B����ͬʱ�������ؾ��εı�DC��CB��BA�����˶�����E���˶��ٶ�Ϊ
����E��F��G�ֱ��D��C��B����ͬʱ�������ؾ��εı�DC��CB��BA�����˶�����E���˶��ٶ�Ϊ![]() ����F���˶��ٶ�Ϊ
����F���˶��ٶ�Ϊ![]() ����G���˶��ٶ�Ϊ
����G���˶��ٶ�Ϊ![]() ������F�����
������F�����![]() ��F���B�غ�
��F���B�غ�![]() ʱ����������ֹ֮ͣ�˶�
ʱ����������ֹ֮ͣ�˶�![]() ���˶������У�
���˶������У�![]() ����ֱ��EF�ĶԳ�ͼ����
����ֱ��EF�ĶԳ�ͼ����![]() ���E��F��G�˶���ʱ��Ϊ
���E��F��G�˶���ʱ��Ϊ![]() ��λ��
���![]()
![]() ��
��![]() ______sʱ���ı���
______sʱ���ı���![]() Ϊ�����Σ�
������
![]() ���Ե�E��C��FΪ��������������Ե�F��B��GΪ��������������ƣ���t��ֵ��
���Ե�E��C��FΪ��������������Ե�F��B��GΪ��������������ƣ���t��ֵ��
![]() �Ƿ����ʵ��t��ʹ�õ�
�Ƿ����ʵ��t��ʹ�õ�![]() ���O�غϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
���O�غϣ������ڣ�ֱ��д��t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ����
��ͼ����![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ���
���![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �͵�
�͵�![]() ���ҵ�
���ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
(1)��![]() ��ֵ��
��ֵ��![]() �ij�;
�ij�;
(2)����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() �����
�����![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
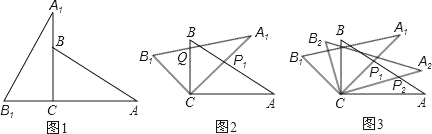
����Ŀ��������ȫ�ȵ����ǰ���ͼ1�ڷţ����С�A1CB1����ACB��90������A1����A��30����
��1����ͼ1����A1B1C�Ƶ�C˳ʱ����ת45����ͼ2����P1��A1C��AB�Ľ��㣬��Q��A1B1��BC�Ľ��㣬��֤��CP1��CQ��
��2����ͼ2�У���AP1��a����CQ���ڶ��٣�
��3����ͼ2����A1B1C����C˳ʱ����ת����A2B2C����ͼ3������P2��A2C��AP1�Ľ��㣮����ת��Ϊ���ٶ�ʱ������AP1C�ס�CP1P2����ʱ�߶�CP1��P1P2֮�����һ��������������ϵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ͼ�λͬѧ���ֵ�Ӱ����Ϸʱ�����ֶ���ͬһ���壬Ӱ�ӵĴ�С���Դ������ľ����й�.��ˣ�������Ϊ�����Խ��������Ӱ�ӳ��ȼ����Դ�������λ��.���ǣ������������³���.
��1����ͼ������ֱ�ڵ�����õ������ο��ABCD���߳�ABΪ30cm���������Ϸ���һ���ݣ��ڵ��ݵ������£������ο�ܵĺ���Ӱ��A��B��D��C�ij��Ⱥ�Ϊ6cm.��ô���������ĸ߶�Ϊ .
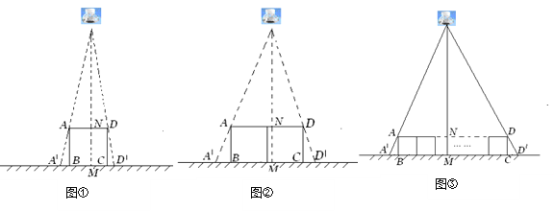 ��2�����ı����е��ݵĸ߶ȣ��������߳�Ϊ30cm�������ο�ܰ�ͼ���ڷţ�������ʱ����Ӱ��A��B��D��C�ij��Ⱥ�Ϊ���٣�
��2�����ı����е��ݵĸ߶ȣ��������߳�Ϊ30cm�������ο�ܰ�ͼ���ڷţ�������ʱ����Ӱ��A��B��D��C�ij��Ⱥ�Ϊ���٣�
��3����n���߳�Ϊa�������ΰ�ͼ���ڷţ���ú���Ӱ��A��B��D��C�ij��Ⱥ�Ϊb,����������ľ���.��д��������̣�����ú�a,b,n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����������ͬʱ��ͬһ�ҳ��вɹ�����������βɹ�����ĵ��۲���ͬ������ÿ�βɹ�����100ǧ�ˣ���ÿ�βɹ�������ȥ100Ԫ��
��1������a��b�ֱ��ʾ���βɹ�����ʱ�ĵ��ۣ���λ��Ԫ/ǧ�ˣ������ú�a��b��ʽ�ӱ�ʾ�������βɹ����ﹲ�踶���� ��Ԫ�������ι������� ��ǧ�˻��
��2�������жϼס������˲ɹ�����ķ�ʽ��һ����ƽ�����۵ͣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
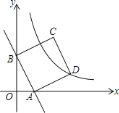
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ཻ�ڵ�
��ֱ��ཻ�ڵ�![]() ��
��![]() ���ı���
���ı���![]() �������Σ�����
�������Σ�����![]() �ڵ�һ��������
�ڵ�һ��������![]() ����˫���߱�ʾ�ĺ�������ʽ��
����˫���߱�ʾ�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�����꼶ѧ����˯������������ȡ�˸������꼶ѧ������ѧ�����е���.��֪D���ѧ����15�ˣ����ó������õ����ݻ�����ʾ��ͳ��ͼ��.
һ��ѧ��˯��������������λ��Сʱ��
��� | ˯��ʱ�� |
|
|
|
|
|
|
|
|
|
|
����ѧ��˯�����ͳ��ͼ
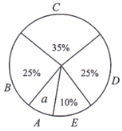
����ͼ���ṩ����Ϣ���ش��������⣺
��1�����������꼶ѧ��˯�����ͳ��ͼ���е�a��ֵ��a��Ӧ�����ε�Բ�ĽǶ�����
��2�����˯��ʱ��x��ʱ�����㣺![]() ����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
����˯��ʱ��ϸ�.��֪�������꼶ѧ����3250�ˣ��Թ��Ƹ������꼶ѧ��˯��ʱ��ϸ�Ĺ��ж����ˣ�
��3������������ѧ��˯������������Сֵ����C����У�ȡ![]() ����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
����B��C��D����ѧ����ƽ��˯��ʱ����Ϊ���꼶ѧ����˯��ʱ�������.����������꼶ѧ����ƽ��˯��ʱ��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com