
【题目】![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() .
.
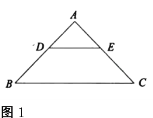
(1)如图1,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 、
、![]() 满足怎样的数量关系和位置关系?(直接写出答案)
满足怎样的数量关系和位置关系?(直接写出答案)
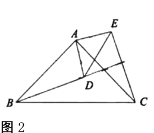
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() 、
、![]() ,则
,则![]() 、
、![]() 满足怎样的数量关系和位置关系?请说明理由.
满足怎样的数量关系和位置关系?请说明理由.
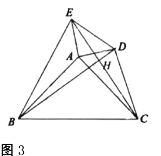
(3)如图3,点![]() 、
、![]() 都在
都在![]() 外部,连结
外部,连结![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.已知
点.已知![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)BD=CE,BD⊥CE;(2)BD=CE,BD⊥CE;证明见解析;(3)y=40-x.
【解析】
(1)根据等腰直角三角形的性质解答;
(2)延长BD,分别交AC、CE于F、G,证明△ABD≌△ACE,根据全等三角形的性质、垂直的定义解答;
(3)先证明∠BAD=∠CAE,再证明△ABD≌△ACE,可得∠BHC =90°,最后利用勾股定理计算即可.
(1)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,
∴BD=CE,BD⊥CE;
(2)BD=CE,BD⊥CE,
理由如下:延长BD,分别交AC、CE于F、G,
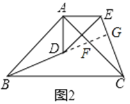
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC
∴∠BAD=∠CAE,
在△ABD和△ACE中,
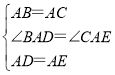 ,
,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE,
∵∠AFB=∠GFC,
∴∠CGF=∠BAF=90°,即BD⊥CE;
(3)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE,
∵∠AOB=∠HOC,
∴∠BHC=∠BAC=90°,
∴CD2+EB2=CH2+HB2+EH2+HD2=BC2+DE2
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE
∵![]() ,
,![]()
∴BC2=32,DE2=8
∵![]() ,
,![]()
∴x+y=32+8
∴y=40-x.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在某隧道建设工程中,需沿![]() 方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点
方向开山修路,为了加快施工进度,要在小山的另一边同时施工.为了使开挖点![]() 在直线
在直线![]() 上,现在
上,现在![]() 上取一点
上取一点![]() ,
,![]() 外取一点
外取一点![]() ,测得
,测得![]() ,
,![]() ,
,![]() .求开挖点
.求开挖点![]() 到点
到点![]() 的距离.
的距离.
(精确到![]() 米)参考数据:
米)参考数据:![]() ,
,![]() ,
,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
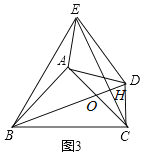
【题目】如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(0,-3),B(3,-2),C(2,-4).
(1)在图中作出△ABC关于x轴对称的△A1B1C1.
(2)点C1的坐标为: .
(3)△ABC的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
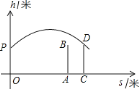
【题目】甲、乙两人同时从相距![]() 千米的
千米的![]() 地匀速前往
地匀速前往![]() 地,甲乘汽车,乙骑电动车,甲到达
地,甲乘汽车,乙骑电动车,甲到达![]() 地停留半个小时后按原速返回
地停留半个小时后按原速返回![]() 地,如图是他们与
地,如图是他们与![]() 地之间的距离
地之间的距离![]() (千米)与经过的时间
(千米)与经过的时间![]() (小时)之间的函数图像.
(小时)之间的函数图像.
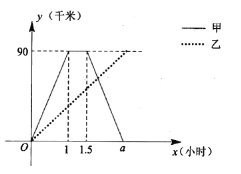
(1)![]() ,并写出它的实际意义 ;
,并写出它的实际意义 ;
(2)求甲从![]() 地返回
地返回![]() 地的过程中
地的过程中![]() 与
与![]() 之间的函数表达式,并写出自变量
之间的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)已知乙骑电动车的速度为![]() 千米/小时,求乙出发后多少小时与甲相遇?
千米/小时,求乙出发后多少小时与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.
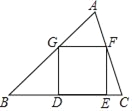
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.等腰三角形的中线与高线重合
C.三边长为![]() 的三角形为直角三角形
的三角形为直角三角形
D.到线段两端距离相等的点在这条线段的垂直平分线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使三角形AMN周长最小时,则∠MAN的度数为_________.
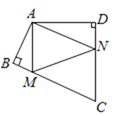
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com