
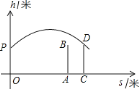
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() .
.
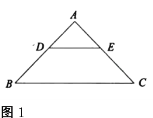
(1)如图1,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 、
、![]() 满足怎样的数量关系和位置关系?(直接写出答案)
满足怎样的数量关系和位置关系?(直接写出答案)
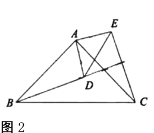
(2)如图2,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,连结
外部,连结![]() 、
、![]() ,则
,则![]() 、
、![]() 满足怎样的数量关系和位置关系?请说明理由.
满足怎样的数量关系和位置关系?请说明理由.
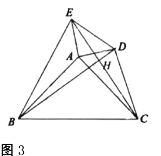
(3)如图3,点![]() 、
、![]() 都在
都在![]() 外部,连结
外部,连结![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 与
与![]() 相交于
相交于![]() 点.已知
点.已知![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:用图象法解一元二次不等式:x2﹣2x﹣3>0
解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.
又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.
观察函数图象可知:当x<﹣1或x>3时,y>0.
∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.
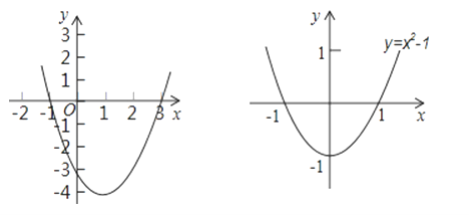
(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3>0的解集是 ________;
(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
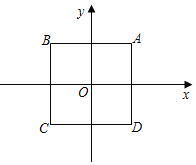
【题目】在平面直角坐标系xOy中,点P到封闭图形F的“极差距离”D(P,W)定义如下:任取图形W上一点Q,记PQ长度的最大值为M,最小值为m(若P与Q重合,则PQ=0),则“极差距离”D(P,W)=M﹣m.如图,正方形ABCD的对角线交点恰与原点O重合,点A的坐标为(2,2)
(1)点O到线段AB的“极差距离”D(O,AB)=______.点K(5,2)到线段AB的“极差距离”D(K,AB)=______.
(2)记正方形ABCD为图形W,点P在x轴上,且“极差距离”D(P,W)=2,求直线AP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,依据作图痕迹回答下面的问题:
,依据作图痕迹回答下面的问题:
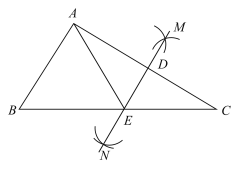
(1)![]() 和
和![]() 的位置关系是_________________;
的位置关系是_________________;
(2)若![]() ,
,![]() 时,求
时,求![]() 的周长;
的周长;
(3)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
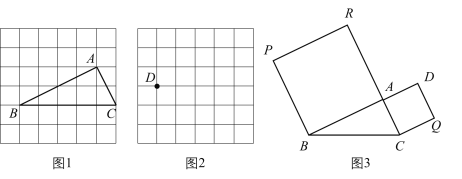
(1)图1中线段![]() 的长是___________;请判断
的长是___________;请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)请在图2中画出![]() ,使
,使![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() .
.
(3)如图3,以图1中![]() 的
的![]() ,
,![]() 为边作正方形
为边作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
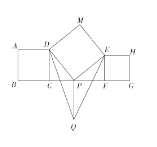
【题目】如图,![]() 为正方形
为正方形![]() 的边
的边![]() 的延长线上一动点,以
的延长线上一动点,以![]() 为一边做正方形
为一边做正方形![]() ,以
,以![]() 为一顶点作正方形
为一顶点作正方形![]() ,且
,且![]() 在
在![]() 的延长线上(提示:正方形四条边相等,且四个内角为
的延长线上(提示:正方形四条边相等,且四个内角为![]() )
)
(1)若正方形![]() 、
、![]() 的面积分别为
的面积分别为![]() ,
,![]() ,则正方形
,则正方形![]() 的面积为 (直接写结果).
的面积为 (直接写结果).
(2)过点![]() 做
做![]() 的垂线交
的垂线交![]() 的平分线于点
的平分线于点![]() ,连接
,连接![]() ,试探求在点
,试探求在点![]() 运动过程中,
运动过程中,![]() 的大小是否发生变化,并说明理由.
的大小是否发生变化,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com