
【题目】如图,已知![]() ,依据作图痕迹回答下面的问题:
,依据作图痕迹回答下面的问题:
(1)![]() 和
和![]() 的位置关系是_________________;
的位置关系是_________________;
(2)若![]() ,
,![]() 时,求
时,求![]() 的周长;
的周长;
(3)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)MN垂直平分AC;(2)8;(3)90°.
【解析】
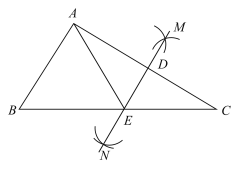
(1)根据作图痕迹可知MN为所作的AC的垂直平分线;
(2)根据垂直平分线的性质可得AE=EC,从而将△ABE周长转化为AB+BC;
(3)由条件可得△ABE是等边三角形,再利用等腰三角形的性质和三角形内角和得出∠BAC的度数.
解:(1)由作图痕迹可知:MN是线段AC的垂直平分线,
∴![]() 和
和![]() 的位置关系是:MN垂直平分AC;
的位置关系是:MN垂直平分AC;
(2)∵MN垂直平分AC,
∴AE=EC,
∵![]() ,
,![]() ,
,
∴△ABE的周长=AB+BE+AE=AB+BC=8;
(3)∵![]() ,
,![]() ,
,
∴△ABE是等边三角形,∠B=∠BAE,
∵AE=EC,
∴∠C=∠EAC,
∵∠B+∠BAE+∠C+∠EAC=180°,
∴∠BAC=∠BAE+∠EAC=90°.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距![]() 千米的
千米的![]() 地匀速前往
地匀速前往![]() 地,甲乘汽车,乙骑电动车,甲到达
地,甲乘汽车,乙骑电动车,甲到达![]() 地停留半个小时后按原速返回
地停留半个小时后按原速返回![]() 地,如图是他们与
地,如图是他们与![]() 地之间的距离
地之间的距离![]() (千米)与经过的时间
(千米)与经过的时间![]() (小时)之间的函数图像.
(小时)之间的函数图像.
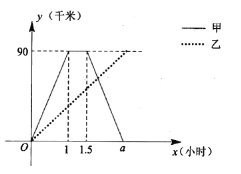
(1)![]() ,并写出它的实际意义 ;
,并写出它的实际意义 ;
(2)求甲从![]() 地返回
地返回![]() 地的过程中
地的过程中![]() 与
与![]() 之间的函数表达式,并写出自变量
之间的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)已知乙骑电动车的速度为![]() 千米/小时,求乙出发后多少小时与甲相遇?
千米/小时,求乙出发后多少小时与甲相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
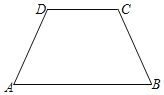
【题目】如图,在四边形ABCD中,AB∥DC,边AD与BC不平行
(1)若∠A=∠B,求证:AD=BC.
(2)已知AD=BC,∠A=70°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
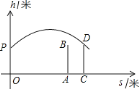
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
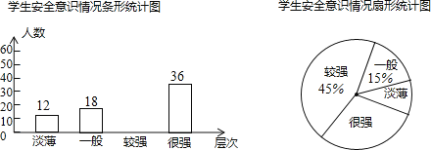
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接全市体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的![]() 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到
名男生中随机抽取了部分男生的测试成绩(单位:米,精确到![]() 米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为
米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为![]() ,其中
,其中![]() 的频数为
的频数为![]() ,请根据有关信息解答下列问题:
,请根据有关信息解答下列问题:
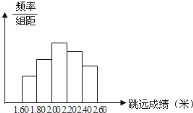
![]() 填空:这次调查的样本容量为________,
填空:这次调查的样本容量为________,![]() 这一小组的频率为________;
这一小组的频率为________;
![]() 请指出样本成绩的中位数落在哪一小组内,并说明理由;
请指出样本成绩的中位数落在哪一小组内,并说明理由;
![]() 样本中男生立定跳远的人均成绩不低于多少米;
样本中男生立定跳远的人均成绩不低于多少米;
![]() 请估计该校初三男生立定跳远成绩在
请估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有多少人?
米)的约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com