
【题目】如图,已知∠A=∠D=90°,点E、F在线段BC上,DE与AF交于点O,且AB=DC,BE=CF.求证:
(1)AF=DE
(2)若OP⊥EF,求证:OP平分∠EOF.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康.你知道吗,被动吸烟也大大危害着人类的健康.为此,联合国规定每年的5月31日为世界无烟日.为配合今年的“世界无烟日”宣传活动,小明和同学们在学校所在地区展开了以“我支持的戒烟方式”为主题的问卷调查活动,征求市民的意见,并将调查结果分析整理后,制成下列统计图:

(1)求小明和同学们一共随机调查了多少人?
(2)根据以上信息,请你把统计图补充完整;
(3)如果该地区有2万人,那么请你根据以上调查结果,估计该地区大约有多少人支持“强制戒烟”这种戒烟方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
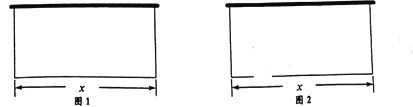
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m .设饲养室为长为x(m),占地面积为![]() .
.
(1)如图![]() ,问饲养室为长x为多少时,占地面积y 最大?
,问饲养室为长x为多少时,占地面积y 最大?
(2)如图![]() ,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在平面直角坐标系中,二元一次方程x-y=0的一个解![]() 可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
直线x-y=0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M(x0,y0)的坐标满足不等式x-y≤0,那么点M(x0,y0)就在直线x-y=0的上方区域内。特别地,x=k(k为常数)表示横坐标为k的点的全体组成的一条直线,y=m(m为常数)表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料,探索完成以下问题:
(1)已知点A(2,1)、B(![]() ,
,![]() )、C(
)、C(![]() ,
,![]() )、D(4,
)、D(4,![]() ),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
(2)已知点P(x,y)的坐标满足不等式组![]() ,则所有的点P组成的图形的面积是 ;
,则所有的点P组成的图形的面积是 ;
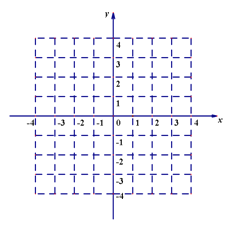
(3)已知点P(x,y)的坐标满足不等式组 ,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
查看答案和解析>>
科目:初中数学 来源: 题型:
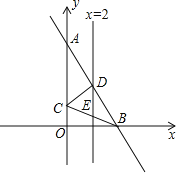
【题目】如图,平面直角坐标系中,直线AB:y=-2x+8交y轴于点A,交x轴于点B,以AB为底作等腰三角形△ABC的顶点C恰好落在y轴上,连接BC,直线x=2交AB于点D,交BC于点E,交x轴于点G,连接CD.
(1)求证:∠OCB=2∠CBA;
(2)求点C的坐标和直线BC的解析式;
(3)求△DEB的面积;
(4)在x轴上存在一点P使PD-PC最长,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
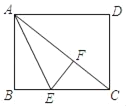
【题目】如图,矩形纸片ABCD中,已知AD=12,AB=9,E是BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】口袋中装有四个大小完全相同的小球,把它们分别标号1,2,3,4,从中随机摸出一个球,记下数字后放回,再从中随机摸出一个球,利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】![]() .
.
【解析】试题分析:
根据题意列表如下,由表可以得到所有的等可能结果,再求出所有结果中,两次所摸到小球的数字之和为4的次数,即可计算得到所求概率.
试题解析:
列表如下:
1 | 2 | 3 | 4 | |
1 | (1,1) | (1,2) | (1,3) | (1,4) |
2 | (2,1) | (2,2) | (2,3) | (2,4) |
3 | (3,1) | (3,2) | (3,3) | (3,4) |
4 | (4,1) | (4,2) | (4,3) | (4,4) |
由表可知,共有16种等可能事件,其中两次摸到的小球数字之和等于4的有(3,1)、(2,2)和(1,3),共计3种,
∴P(两次摸到小球的数字之和等于4)=![]() .
.
【题型】解答题
【结束】
23
【题目】小亮同学想利用影长测量学校旗杆AB的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上BD处,另一部分在某一建筑的墙上CD处,分别测得其长度为9.6米和2米,求旗杆AB的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com