
【题目】为了迎接全市体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的![]() 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到
名男生中随机抽取了部分男生的测试成绩(单位:米,精确到![]() 米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为
米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为![]() ,其中
,其中![]() 的频数为
的频数为![]() ,请根据有关信息解答下列问题:
,请根据有关信息解答下列问题:
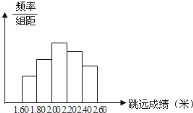
![]() 填空:这次调查的样本容量为________,
填空:这次调查的样本容量为________,![]() 这一小组的频率为________;
这一小组的频率为________;
![]() 请指出样本成绩的中位数落在哪一小组内,并说明理由;
请指出样本成绩的中位数落在哪一小组内,并说明理由;
![]() 样本中男生立定跳远的人均成绩不低于多少米;
样本中男生立定跳远的人均成绩不低于多少米;
![]() 请估计该校初三男生立定跳远成绩在
请估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有多少人?
米)的约有多少人?
【答案】(1)![]() ;(2)中位数落在
;(2)中位数落在![]() 这一小组内;(3)样本中男生立定跳远的人均成绩不低于
这一小组内;(3)样本中男生立定跳远的人均成绩不低于![]() 米;(4)该校初三男生立定跳远成绩在
米;(4)该校初三男生立定跳远成绩在![]() 米以上的约有
米以上的约有![]() 人.
人.
【解析】
(1)每小组的频率=小组的频数÷总人数.第2小组的频数为8;这5个小组频率之比为2:4:6:5:3,可求得第2组频率为0.2;即可求的样本容量即总人数;
(2)根据中位数的求法,将数据从小到大排列,找最中间两个数的平均数即可得出答案;
(3)计算其平均数即可得答案;
(4)用样本估计总体.
(1)样本容量=(2+4+6+5+3)÷4×8=40;![]() =3÷20=0.15;
=3÷20=0.15;
![]() ∵各小组的频数分别为:
∵各小组的频数分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而中位数是![]() 个成绩从小到大排列后第
个成绩从小到大排列后第![]() 个数据和第
个数据和第![]() 个数据的平均数,
个数据的平均数,
∴中位数落在![]() 这一小组内;
这一小组内;
![]() 设样本人均成绩最低值为
设样本人均成绩最低值为![]() ,
,
则![]() ,
,
∴样本中男生立定跳远的人均成绩不低于![]() 米;
米;
![]() 估计该校初三男生立定跳远成绩在
估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有
米)的约有![]() (人))
(人))
所以该校初三男生立定跳远成绩在![]() 米以上的约有
米以上的约有![]() 人.
人.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,依据作图痕迹回答下面的问题:
,依据作图痕迹回答下面的问题:
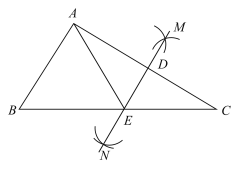
(1)![]() 和
和![]() 的位置关系是_________________;
的位置关系是_________________;
(2)若![]() ,
,![]() 时,求
时,求![]() 的周长;
的周长;
(3)若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,在AD上取点E,使DE=CD,连结BE.求证:BE=AC.
问题拓展:如图②,在问题原型的条件下,F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM.
(1)判断线段AC与CM的大小关系,并说明理由.
(2)若AC=![]() ,直接写出A、M两点之间的距离.
,直接写出A、M两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙、丙三个厂家生产的同一种产品中,各抽出![]() 件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
三家广告中都称该种产品的使用寿命是![]() 年,请根据调查结果判断三个厂家在广告中分别运用了平均数,众数和中位数的哪一种数据作代表.
年,请根据调查结果判断三个厂家在广告中分别运用了平均数,众数和中位数的哪一种数据作代表.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
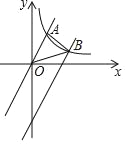
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的大学生自愿者参与服务工作,计划组织全校自愿者统一乘车去某地.若单独调配![]() 座客车若干辆,则空出
座客车若干辆,则空出![]() 个座位,若只调配
个座位,若只调配![]() 座客车若干辆,则用车数量将增加
座客车若干辆,则用车数量将增加![]() 辆,并有
辆,并有![]() 人没有座位.
人没有座位.
(1)计划调配![]() 座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
座客车多少辆?该大学共有多少名自愿者?(列方程组解答)
(2)若同时调配![]() 座和
座和![]() 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com