
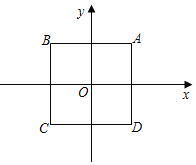
【题目】在平面直角坐标系xOy中,点P到封闭图形F的“极差距离”D(P,W)定义如下:任取图形W上一点Q,记PQ长度的最大值为M,最小值为m(若P与Q重合,则PQ=0),则“极差距离”D(P,W)=M﹣m.如图,正方形ABCD的对角线交点恰与原点O重合,点A的坐标为(2,2)
(1)点O到线段AB的“极差距离”D(O,AB)=______.点K(5,2)到线段AB的“极差距离”D(K,AB)=______.
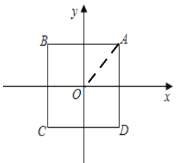
(2)记正方形ABCD为图形W,点P在x轴上,且“极差距离”D(P,W)=2,求直线AP的解析式.
【答案】(1)2![]() ﹣2;4;(2)y=
﹣2;4;(2)y=![]() x﹣1或y=
x﹣1或y=![]() x+
x+![]() .
.
【解析】
(1)由题意得出M=OA=2![]() ,m=2,即可得出O到线段AB的“极差距离”;由题意得出AK=3,BK=7,则M=BK=7,m=AK=3,即可得出结果;
,m=2,即可得出O到线段AB的“极差距离”;由题意得出AK=3,BK=7,则M=BK=7,m=AK=3,即可得出结果;
(2)由题意得出点P的坐标为(8,0)或(﹣8,0),设直线AP的解析式为:y=kx+a,代入点A、点P的坐标即可得出解析式.
解:(1)∵点A的坐标为(2,2),正方形ABCD的对角线交点恰与原点O重合,
∴OA=![]() ,
,
∴M=OA=2![]() ,m=2,
,m=2,
∴O到线段AB的“极差距离”D(O,AB)=![]() ;
;
∵点K(5,2),如图1所示:
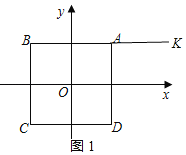
∴AK=3,BK=7,
∴M=BK=7,m=AK=3,
∴点K(5,2)到线段AB的“极差距离”D(K,AB)=4;
故答案为:2![]() ﹣2;4;
﹣2;4;
(2)设点P(x,0),
若点P在O的右侧,则M=BP,m=PN=2﹣x,BH=2,PH=x+2,如图2所示:
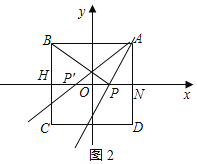
∵“极差距离”D(P,W)=2,
∴![]() ﹣(2﹣x)=2,
﹣(2﹣x)=2,
解得:x=![]() ,
,
同理,点P在O的左侧,x=![]() ,
,
∴点P的坐标为(![]() ,0)或(﹣
,0)或(﹣![]() ,0),
,0),
设直线AP的解析式为:y=kx+a,
当点P的坐标为(![]() ,0)时,则:
,0)时,则:
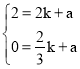 ,解得:
,解得: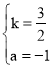 ,
,
∴此时,直线AP的解析式为y=![]() x﹣1;
x﹣1;
当点P的坐标为(﹣![]() ,0)时,则:
,0)时,则:
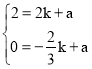 ,解得:
,解得:![]() ,
,
∴此时,直线AP的解析式为y=![]() x+
x+![]() ;
;
∴直线AP的解析式为:y=![]() x﹣1或y=
x﹣1或y=![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
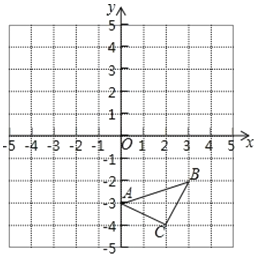
【题目】如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(0,-3),B(3,-2),C(2,-4).
(1)在图中作出△ABC关于x轴对称的△A1B1C1.
(2)点C1的坐标为: .
(3)△ABC的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使三角形AMN周长最小时,则∠MAN的度数为_________.
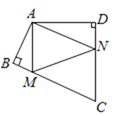
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,边AD与BC不平行
(1)若∠A=∠B,求证:AD=BC.
(2)已知AD=BC,∠A=70°,求∠B的度数.
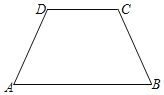
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有![]() 个红球和
个红球和![]() 个白球,每个球除颜色外,其余特征均相同.
个白球,每个球除颜色外,其余特征均相同.
![]() 任意摸出
任意摸出![]() 个球,摸出红球的概率是多少?
个球,摸出红球的概率是多少?
![]() 任意摸出
任意摸出![]() 个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
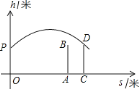
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
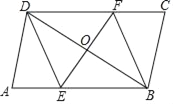
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宝安区某街道对长为20千米的路段进行排水管道改造后,需对该段路面全部重新进行修整,甲、乙两个工程队将参与施工,已知甲队每天的工作效率是乙队的2倍,若由甲、乙两队分别单独修整长为800米的路面,甲队比乙队少用5天.
(1)求甲队每天可以修整路面多少米?
(2)若街道每天需支付给甲队的施工费用为0.4万元,乙队为0.25万元,如果本次路面修整预算55万元,为了不超出预算,至少应该安排甲队参与工程多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com