
【题目】如果一边长为![]() 的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,那么铁圈直径的最小值为________
的等边三角形硬纸板刚好能不受损地从用铁丝围成的圆形铁圈中穿过,那么铁圈直径的最小值为________![]() (铁丝粗细忽略不计).
(铁丝粗细忽略不计).
科目:初中数学 来源: 题型:
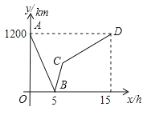
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,慢车的速度是快车速度的![]() ,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象解决以下问题:
(1)甲、乙两地之间的距离为 km;D点的坐标为 ;
(2)求线段BC的函数关系式,并写出自变量x的取值范围;
(3)若第二列快车从乙地出发驶往甲地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车追上慢车.求第二列快车比第一列快车晚出发多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 两地相距
两地相距![]() 千米,甲、乙两人都从
千米,甲、乙两人都从![]() 地去
地去![]() 地,图中
地,图中![]() 和
和![]() 分别表示甲、乙两人所走路程
分别表示甲、乙两人所走路程![]() (千米)与时间
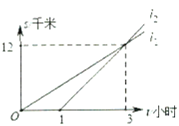
(千米)与时间![]() (小时)之间的关系,下列说法: ①乙晚出发
(小时)之间的关系,下列说法: ①乙晚出发![]() 小时;②乙出发
小时;②乙出发![]() 小时后追上甲;③甲的速度是
小时后追上甲;③甲的速度是![]() 千米/小时; ④乙先到达
千米/小时; ④乙先到达![]() 地.其中正确的是__________.(填序号)
地.其中正确的是__________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题:
(1)当x=3时,y=________;
(2)当x=_____时,y有最________值为________;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且﹣1<x1<0,1<x2<2,试比较两函数值的大小:y1________y2 ;
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:用图象法解一元二次不等式:x2﹣2x﹣3>0
解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.
又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.
∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.
观察函数图象可知:当x<﹣1或x>3时,y>0.
∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.
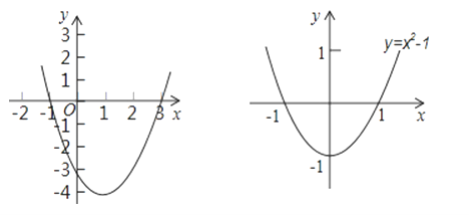
(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3>0的解集是 ________;
(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
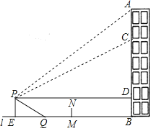
【题目】如图,重庆某广场新建与建筑物![]() 垂直的空中玻璃走廊
垂直的空中玻璃走廊![]() 与
与![]() 相连,
相连,![]() 与地面
与地面![]() 垂直.在
垂直.在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,测得建筑物
,测得建筑物![]() 处的仰角为
处的仰角为![]() (不计测量人员的身高),
(不计测量人员的身高),![]() 为
为![]() 米.图中的点
米.图中的点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 及直线
及直线![]() 均在同一平面内.
均在同一平面内.
![]() 求
求![]() 、
、![]() 两点的高度差(结果精确到
两点的高度差(结果精确到![]() 米);
米);
![]() 为方便游客,广场从地面
为方便游客,广场从地面![]() 上的
上的![]() 点新建扶梯
点新建扶梯![]() ,
,![]() 所在斜面的坡度
所在斜面的坡度![]() ,
,![]() 到地面
到地面![]() 的距离
的距离![]() 为
为![]() 米.一广告牌
米.一广告牌![]() 位于
位于![]() 的中点
的中点![]() 处,市政规划要求在点
处,市政规划要求在点![]() 右侧需留出
右侧需留出![]() 米的行车道,请判断是否需要挪走广告牌
米的行车道,请判断是否需要挪走广告牌![]() ,并说明理由.(参考数据:
,并说明理由.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
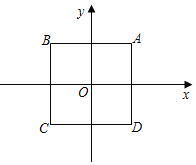
【题目】在平面直角坐标系xOy中,点P到封闭图形F的“极差距离”D(P,W)定义如下:任取图形W上一点Q,记PQ长度的最大值为M,最小值为m(若P与Q重合,则PQ=0),则“极差距离”D(P,W)=M﹣m.如图,正方形ABCD的对角线交点恰与原点O重合,点A的坐标为(2,2)
(1)点O到线段AB的“极差距离”D(O,AB)=______.点K(5,2)到线段AB的“极差距离”D(K,AB)=______.
(2)记正方形ABCD为图形W,点P在x轴上,且“极差距离”D(P,W)=2,求直线AP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
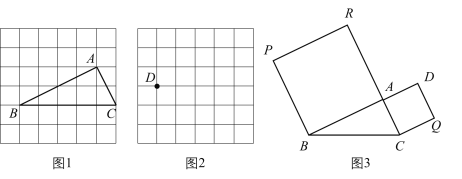
(1)图1中线段![]() 的长是___________;请判断
的长是___________;请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)请在图2中画出![]() ,使
,使![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() .
.
(3)如图3,以图1中![]() 的
的![]() ,
,![]() 为边作正方形
为边作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com