
【题目】一个不透明的袋中装有![]() 个红球和
个红球和![]() 个白球,每个球除颜色外,其余特征均相同.
个白球,每个球除颜色外,其余特征均相同.
![]() 任意摸出
任意摸出![]() 个球,摸出红球的概率是多少?
个球,摸出红球的概率是多少?
![]() 任意摸出
任意摸出![]() 个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题:
(1)当x=3时,y=________;
(2)当x=_____时,y有最________值为________;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且﹣1<x1<0,1<x2<2,试比较两函数值的大小:y1________y2 ;
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
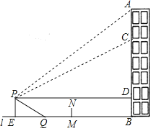
【题目】如图,重庆某广场新建与建筑物![]() 垂直的空中玻璃走廊
垂直的空中玻璃走廊![]() 与
与![]() 相连,
相连,![]() 与地面
与地面![]() 垂直.在
垂直.在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,测得建筑物
,测得建筑物![]() 处的仰角为
处的仰角为![]() (不计测量人员的身高),
(不计测量人员的身高),![]() 为
为![]() 米.图中的点
米.图中的点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 及直线
及直线![]() 均在同一平面内.
均在同一平面内.
![]() 求
求![]() 、
、![]() 两点的高度差(结果精确到
两点的高度差(结果精确到![]() 米);
米);
![]() 为方便游客,广场从地面
为方便游客,广场从地面![]() 上的
上的![]() 点新建扶梯
点新建扶梯![]() ,
,![]() 所在斜面的坡度
所在斜面的坡度![]() ,
,![]() 到地面
到地面![]() 的距离
的距离![]() 为
为![]() 米.一广告牌
米.一广告牌![]() 位于
位于![]() 的中点
的中点![]() 处,市政规划要求在点
处,市政规划要求在点![]() 右侧需留出
右侧需留出![]() 米的行车道,请判断是否需要挪走广告牌
米的行车道,请判断是否需要挪走广告牌![]() ,并说明理由.(参考数据:
,并说明理由.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
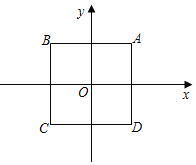
【题目】在平面直角坐标系xOy中,点P到封闭图形F的“极差距离”D(P,W)定义如下:任取图形W上一点Q,记PQ长度的最大值为M,最小值为m(若P与Q重合,则PQ=0),则“极差距离”D(P,W)=M﹣m.如图,正方形ABCD的对角线交点恰与原点O重合,点A的坐标为(2,2)
(1)点O到线段AB的“极差距离”D(O,AB)=______.点K(5,2)到线段AB的“极差距离”D(K,AB)=______.
(2)记正方形ABCD为图形W,点P在x轴上,且“极差距离”D(P,W)=2,求直线AP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.
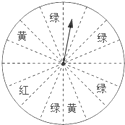
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
方格纸中的位置如图1所示,方格纸中的每个小正方形的边长为1个单位长度.
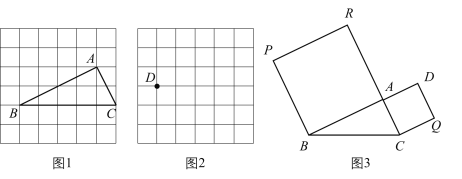
(1)图1中线段![]() 的长是___________;请判断
的长是___________;请判断![]() 的形状,并说明理由.
的形状,并说明理由.
(2)请在图2中画出![]() ,使
,使![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() ,
,![]() ,
,![]() .
.
(3)如图3,以图1中![]() 的
的![]() ,
,![]() 为边作正方形
为边作正方形![]() 和正方形
和正方形![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
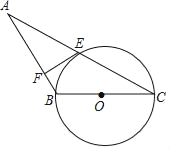
【题目】如图所示,在△ABC中,AB=CB,以BC为直径的⊙O交AC于点E,过点E作⊙O的切线交AB于点F.
(1)求证:EF⊥AB;
(2)若AC=16,⊙O的半径是5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是 ;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、 92、85.
①这组数据的众数是 ,中位数是 ;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com