【题目】在一次促销活动中，某商场为了吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被平均分成
份），并规定：顾客每购买
元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得
元、
元、
元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券
元．
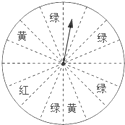
（1）求每转动一次转盘所获购物券金额的平均数；
（2）如果你在该商场消费
元，你会选择转转盘还是直接获得购物券？说明理由．
科目：初中数学 来源： 题型：
【题目】某学校后勤人员到一家文具店给九年级的同学购买考试用文具包，文具店规定一次购买400个以上，可享受8折优惠.若给九年级学生每人购买一个，不能享受8折优惠，需付款1936元；若多买88个，就可享受8折优惠，同样只需付款1936元.请问该学校九年级学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
经过点A（
，0），B（
，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】关于x的一元二次方程x2+（k﹣5）x+1﹣k=0，其中k为常数．
（1）求证：无论k为何值，方程总有两个不相等实数根；
（2）若原方程的一根大于3，另一根小于3，求k的最大整数值．
查看答案和解析>>
科目：初中数学 来源： 题型：
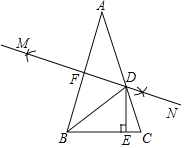
【题目】如图，在△ABC中，AB＝AC，∠A＝36°，分别以A和B为圆心，大于
AB的长为半径作弧，两弧相交于M，N两点，作直线MN分别交AB、AC于点F、D，作DE⊥BC于E．有下面三个结论：①BD平分∠ABC;②DE＝DF;③BC+CD＝2AF;其中，正确的结论的个数是（ ）
A.3B.2C.1D.0
查看答案和解析>>
科目：初中数学 来源： 题型：
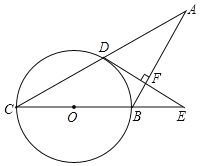
【题目】如图，在等腰△ABC中，AB=BC，以BC为直径的⊙O与AC相交于点D，过点D作DE⊥AB交CB延长线于点E，垂足为点F．
（1）判断DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径R=5，tanC=
，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，D是AB上的点，过点D作
交BC于点F，交AC的延长线于点E，连接CD，
，则下列结论正确的有（ ）
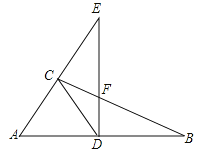
①∠DCB=∠B；②CD=
AB；③△ADC是等边三角形；④若∠E=30°，则DE=EF+CF．
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
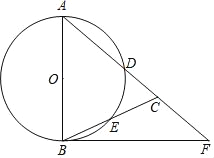
【题目】如图，在△ABC中，AB＝AC，以AB为直径作⊙O，分别交AC、BC于点D、E，点F在AC的延长线上，且∠A＝2∠CBF．
(1)求证：BF与⊙O相切．
(2)若BC＝CF＝4，求BF的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
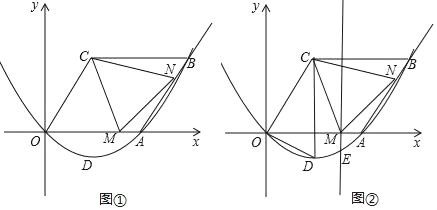
【题目】如图抛物线y=ax2+bx，过点A（4，0）和点B（6，2
），四边形OCBA是平行四边形，点M（t，0）为x轴正半轴上的点，点N为射线AB上的点，且AN=OM，点D为抛物线的顶点．
（1）求抛物线的解析式，并直接写出点D的坐标；
（2）当△AMN的周长最小时，求t的值；
（3）如图②，过点M作ME⊥x轴，交抛物线y=ax2+bx于点E，连接EM，AE，当△AME与△DOC相似时．请直接写出所有符合条件的点M坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
