
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
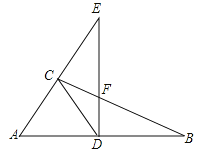
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】B
【解析】
由在△ABC中,∠ACB=90°,DE⊥AB,根据等角的余角相等,可得①∠DCB=∠B正确;
由①可证得AD=BD=CD,即可得②CD=![]() AB正确;
AB正确;
易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;
由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.
在△ABC中,∵∠ACB=90°,DE⊥AB,∴∠ADE=∠ACB=90°,∴∠A+∠B=90°,∠ACD+∠DCB=90°.
∵∠DCA=∠DAC,∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD.
∵AD=BD,∴CD=![]() AB;故②正确;
AB;故②正确;
∠DCA=∠DAC,∴AD=CD,但不能判定△ADC是等边三角形;故③错误;
∵∠E=30°,∴∠A=60°,∴△ACD是等边三角形,∴∠ADC=30°.
∵∠ADE=∠ACB=90°,∴∠EDC=∠BCD=∠B=30°,∴CF=DF,∴DE=EF+DF=EF+CF.故④正确.
故选B.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
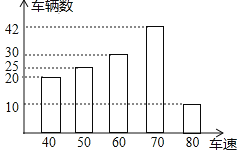
A. 众数是80千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
B. 众数是70千米![]() 时,中位数是70千米
时,中位数是70千米![]() 时
时
C. 众数是60千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
D. 众数是70千米![]() 时,中位数是60千米
时,中位数是60千米![]() 时
时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七、八年级学生的睡眠情况,随机抽取了该校七、八年级部分学生进行调查.已知抽取的七年级与八年级的学生人数相同,利用抽样所得的数据绘制了如下统计图表.

根据图表提供的信息,回答下列问题:
(1)求统计图中的a.
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人.如果睡眠时间x(小时)满足:7.5≤x<9.5,称睡眠时间合格.试估计该校七、八年级学生中睡眠时间合格的共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: 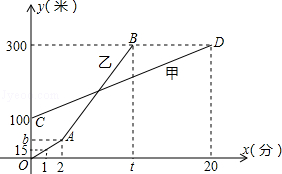
(1)甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
查看答案和解析>>
科目:初中数学 来源: 题型:
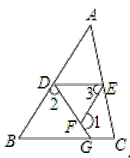
【题目】完成下列推理过程:
已知:如图,∠1+∠2=180°,∠3=∠B
求证:∠EDG+∠DGC=180°
证明:∵∠1+∠2=180°(已知)
∠1+∠DFE=180°( )
∴∠2= ( )
∴EF∥AB( )
∴∠3= ( )
又∵∠3=∠B(已知)
∴∠B=∠ADE( )
∴DE∥BC( )
∴∠EDG+∠DGC=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
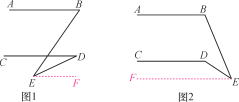
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com