
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
【答案】(1)见解析(2) 279
【解析】试题分析:(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量4≤x<5所占百分比和频数,月均用水量6≤x<7的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
试题解析:(1)调查的总数是50户,
则6≤x<7的户数是50×12%=6(户),
则4≤x<5的户数是50-2-12-10-6-3-2=15(户),
所占的百分比是![]() ×100%=30%.
×100%=30%.
补全频数分布表如下:
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | 15 | 30% |
5≤x<6 | 10 | 20% |
6≤x<7 | 6 | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
补全频数分布直方图如图.
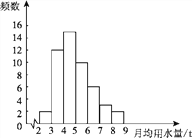
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户).


科目:初中数学 来源: 题型:
【题目】已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为E、F,点O为AC的中点.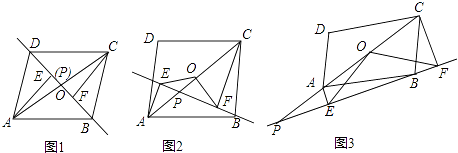
(1)当点P与点O重合时如图1,求证:OE=OF
(2)直线BP绕点B逆时针方向旋转,当点P在对角线AC上时,且∠OFE=30°时,如图2,猜想线段CF、AE、OE之间有怎样的数量关系?并给予证明.
(3)当点P在对角线CA的延长线上时,且∠OFE=30°时,如图3,猜想线段CF、AE、OE之间有怎样的数量关系?直接写出结论即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:ΔABF≌ΔEDF;
(2)将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,.求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线相互垂直的四边形
C.正方形
D.对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
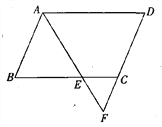
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.已知AB=4,BC=6,∠F=55°,求线段EC的长和∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.

(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是______数(填“无理”或“有理”),这个数是______;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是______;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,-5,+4,+3,-2当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(2,0),以OA为一边在第四象限内画正方形OABC,D(m,0)为x轴上的一个动点,以BD为一边画正方形BDFE(点E在直线x=2的右侧).
(1)当m>2时(如图1),试判断线段AE与CD的数量关系,并说明理由.
(2)当AE=![]() 时,求点F的坐标.
时,求点F的坐标.
(3)连接CF、OF,请直接写出CF+OF的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com