
【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:ΔABF≌ΔEDF;
(2)将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,.求DG的长.
【答案】
(1)
证明:在矩形ABCD中,AB=CD, ![]()
由折叠的性质可知:DE=CD, ![]()
∴AB=DE, ![]() ,
,
又∵ ![]()
∴△ABF≌△EDF(AAS)
(2)
解:∵AD//BC,
∴ ![]() ,
,
由折叠的性质可知: ![]()
∴ ![]()
∴BG=DG
设GC为 ![]() ,则BG=DG=8-
,则BG=DG=8- ![]()
在Rt△DCG中,由勾股定理可得: ![]()
解得: ![]()
【解析】(1)根据折叠的性质进行解答,显然有 ![]() BDC≌
BDC≌ ![]() BDE,其对应的边相等,CD=ED,四边形ABCD是矩形,则有AB=ED。易证∠A=∠E,∠AFB=∠EFD,然后根据全等三角形的判断证明△ABF≌△EDF。(2)应用折叠的性质
BDE,其对应的边相等,CD=ED,四边形ABCD是矩形,则有AB=ED。易证∠A=∠E,∠AFB=∠EFD,然后根据全等三角形的判断证明△ABF≌△EDF。(2)应用折叠的性质 ![]() ,BG=DG。设GC为x,表示出DG。已知DC=6,根据勾股定理求出x的值,进而求出DG的长度。
,BG=DG。设GC为x,表示出DG。已知DC=6,根据勾股定理求出x的值,进而求出DG的长度。
【考点精析】本题主要考查了翻折变换(折叠问题)的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】课本中有一个例题: 有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2 .
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题: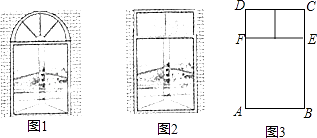
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B,顶点为C,将抛物线在A,C,B之间的部分记为图象E(A,B两点除外).
(1)求抛物线的顶点坐标.
(2)AB=6时,经过点C的直线y=kx+b(k≠0)与图象E有两个交点,结合函数的图象,求k的取值范围.
(3)若横、纵坐标都是整数的点叫整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,C,B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题:
运动项目 | 频数(人数) | 频率 |
篮球 | 20 | 0.40 |
乒乓球 | n | 0.10 |
足球 | 10 | m |
其他 | 15 | 0.30 |
合计 | a | 1.00 |
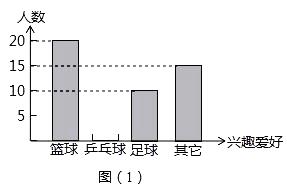
(1)填空: a=;m=;n=;
(2)请将条形统计图补充完整;
(3)该校共有学生1500人,估计参加乒乓球项目的学生有人;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学期结束前,学校想调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
(1)计算出每一种意见的人数占调查人数的百分比;
(2)从统计图中你能得出什么结论?
意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
人数 | 200 | 160 | 32 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |

(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第(100)个图案有___________________个三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=67.5°,BC=4,BE⊥CA于E,CF⊥AB于F,D是BC的中点.以F为原点,FD所在直线为x轴构造平面直角坐标系,则点E的坐标是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com