
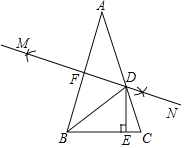
【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于![]() AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
A.3B.2C.1D.0
【答案】A
【解析】
先根据等腰三角形的性质和三角形内角和得到∠ABC=∠C=72°,再利用基本作图得到MN垂直平分AB,则DA=DB,所以∠DBA=∠A=36°,于是可对①进行判断;接着根据角平分线的性质可对②进行判断;通过计算出∠BDC=72°得到∠BDC=∠C,则BC=BD=AD,所以BC+CD=AC=AB,然后利用AB=2AF可对③进行判断.
解:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
由作法得MN垂直平分AB,
∴DA=DB,
∴∠DBA=∠A=36°,
∴BD平分∠ABC,所以①正确;
∵DF⊥BF,DE⊥BE,
∴DE=DF,所以②正确;
∵∠BDC=∠A+∠ABD=36°+36°=72°,
∴∠BDC=∠C,
∴BC=BD=AD,
∴BC+CD=AC=AB,
∵MN垂直平分AB
∴AB=2AF,
∴BC+CD=2AF,所以③正确.
故选:A.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】分解因式2a(b+c)-3(b+c)的结果是______.
【答案】(b+c)(2a-3)
【解析】解析:2a(b+c)-3(b+c)=(b+c)(2a-3).
点睛:因式分解的方法:(1)提取公因式法.ma+mb+mc=m(a+b+c).
(2)公式法:完全平方公式,平方差公式.
(3)十字相乘法.
因式分解的时候,要注意整体换元法的灵活应用,训练将一个式子看做一个整体,利用上述方法因式分解的能力.
【题型】填空题
【结束】
17
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请参照下面探究过程,完成所提出的问题.
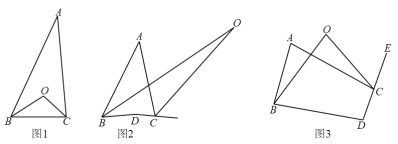
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点.
若∠A=30°,则∠BOC= ;
若∠A=α,则∠BOC= (用含α的代数式表示)
(2)如图2,在四边形ABDC中,点O是∠ABD和∠ACD外角平分线的交点,写出∠A、∠D与∠O之间的数量关系,并说明理由;
(3) 如图3,在四边形ABDC中,∠ABD和∠ACD外角的n等分线交于O,使∠ABD=n∠ABO,∠ACE=n∠ACO.直接写出∠A、∠D和∠O之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.

(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300![]() m2,求EF的长度;
m2,求EF的长度;
(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
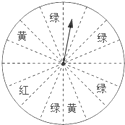
【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成![]() 份),并规定:顾客每购买
份),并规定:顾客每购买![]() 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得![]() 元、
元、![]() 元、
元、![]() 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券![]() 元.
元.
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费![]() 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为4cm,点P,Q分别是直线AB,BC上的动点.
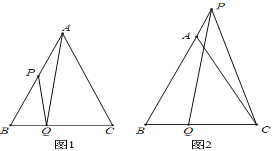
(1)如图1,当点P从顶点A沿AB向B点运动,点Q同时从顶点B沿BC向C点运动,它们的速度都为lcm/s,到达终点时停止运动.设它们的运动时间为t秒,连接AQ,PQ.
①当t=2时,求∠AQP的度数.
②当t为何值时△PBQ是直角三角形?
(2)如图2,当点P在BA的延长线上,Q在BC上,若PQ=PC,请判断AP,CQ和AC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 |
|
|
(1)完成上表;
(2)若从盒子中随机摸出一个球,则摸到白球的概率P= ;(结果保留小数点后一位)
(3)估算这个不透明的盒子里白球有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com