
【题目】已知等边△ABC的边长为4cm,点P,Q分别是直线AB,BC上的动点.
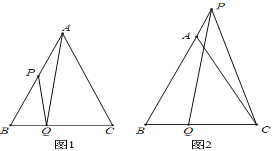
(1)如图1,当点P从顶点A沿AB向B点运动,点Q同时从顶点B沿BC向C点运动,它们的速度都为lcm/s,到达终点时停止运动.设它们的运动时间为t秒,连接AQ,PQ.
①当t=2时,求∠AQP的度数.
②当t为何值时△PBQ是直角三角形?
(2)如图2,当点P在BA的延长线上,Q在BC上,若PQ=PC,请判断AP,CQ和AC之间的数量关系,并说明理由.
【答案】(1)①∠AQP=30°;②当t=![]() 秒或t=
秒或t=![]() 秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由见解析.
秒时,△PBQ为直角三角形;(2)AC=AP+CQ,理由见解析.
【解析】
(1)①由△ABC是等边三角形知AQ⊥BC,∠B=60°,从而得∠AQB=90°,△BPQ是等边三角形,据此知∠BQP=60°,继而得出答案;
②由题意知AP=BQ=t,PB=4﹣t,再分∠PQB=90°和∠BPQ=90°两种情况分别求解可得.
(2)过点Q作QF∥AC,交AB于F,知△BQF是等边三角形,证∠QFP=∠PAC=120°、∠BPQ=∠ACP,从而利用AAS可证△PQF≌△CPA,得AP=QF,据此知AP=BQ,根据BQ+CQ=BC=AC可得答案.
解:(1)①根据题意得AP=PB=BQ=CQ=2,
∵△ABC是等边三角形,
∴AQ⊥BC,∠B=60°,
∴∠AQB=90°,△BPQ是等边三角形,
∴∠BQP=60°,
∴∠AQP=∠AQB﹣∠BQP=90°﹣60°=30°;
②由题意知AP=BQ=t,PB=4﹣t,
当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得:4﹣t=2t,解得t=![]() ;
;
当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(4﹣t),解得t=![]() ;
;
∴当t=![]() 秒或t=
秒或t=![]() 秒时,△PBQ为直角三角形;
秒时,△PBQ为直角三角形;
(2)AC=AP+CQ,理由如下:
如图所示,过点Q作QF∥AC,交AB于F,
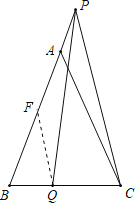
则△BQF是等边三角形,
∴BQ=QF,∠BQF=∠BFQ=60°,
∵△ABC为等边三角形,
∴BC=AC,∠BAC=∠BFQ=60°,
∴∠QFP=∠PAC=120°,
∵PQ=PC,
∴∠QCP=∠PQC,
∵∠QCP=∠B+∠BPQ,∠PQC=∠ACB+∠ACP,∠B=∠ACB,
∴∠BPQ=∠ACP,
在△PQF和△CPA中,
∵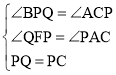
∴△PQF≌△CPA(AAS),
∴AP=QF,
∴AP=BQ,
∴BQ+CQ=BC=AC,
∴AP+CQ=AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于![]() AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
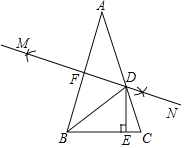
A.3B.2C.1D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有( )
,则下列结论正确的有( )
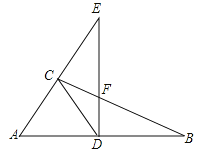
①∠DCB=∠B;②CD=![]() AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
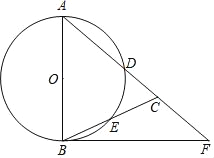
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com