
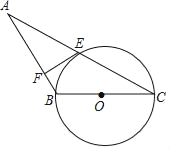
【题目】如图所示,在△ABC中,AB=CB,以BC为直径的⊙O交AC于点E,过点E作⊙O的切线交AB于点F.
(1)求证:EF⊥AB;
(2)若AC=16,⊙O的半径是5,求EF的长.
【答案】(1)证明见解析;(2) 4.8.
【解析】
(1)连结OE,根据等腰三角形的性质可得∠OEC=∠OCA、∠A=∠OCA,即可得∠A=∠OEC,由同位角相等,两直线平行即可判定OE∥AB,又因EF是⊙O的切线,根据切线的性质可得EF⊥OE,由此即可证得EF⊥AB;(2)连结BE,根据直径所对的圆周角为直角可得,∠BEC=90°,再由等腰三角形三线合一的性质求得AE=EC =8,在Rt△BEC中,根据勾股定理求的BE=6,再由△ABE的面积=△BEC的面积,根据直角三角形面积的两种表示法可得8×6=10×EF,由此即可求得EF=4.8.
(1)证明:连结OE.
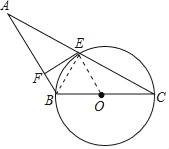
∵OE=OC,
∴∠OEC=∠OCA,
∵AB=CB,
∴∠A=∠OCA,
∴∠A=∠OEC,
∴OE∥AB,
∵EF是⊙O的切线,
∴EF⊥OE,
∴EF⊥AB.
(2)连结BE.
∵BC是⊙O的直径,
∴∠BEC=90°,
又AB=CB,AC=16,
∴AE=EC=![]() AC=8,
AC=8,
∵AB=CB=2BO=10,
∴BE=![]() ,
,
又△ABE的面积=△BEC的面积,即8×6=10×EF,
∴EF=4.8.


科目:初中数学 来源: 题型:
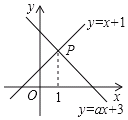
【题目】如图,已知函数y=x+1和y=ax+3的图象交于点P,点P的横坐标为1,
(1)关于x,y的方程组![]() 的解是 ;
的解是 ;
(2)a= ;
(3)求出函数y=x+1和y=ax+3的图象与x轴围成的几何图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有![]() 个红球和
个红球和![]() 个白球,每个球除颜色外,其余特征均相同.
个白球,每个球除颜色外,其余特征均相同.
![]() 任意摸出
任意摸出![]() 个球,摸出红球的概率是多少?
个球,摸出红球的概率是多少?
![]() 任意摸出
任意摸出![]() 个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
个球,摸到红球小明胜,摸出白球小刚胜,这个游戏公平吗?如果不公平,请你在此基础上设计一个公平的游戏,并说明你的设计理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图分别是两根木棒及其影子的情形.
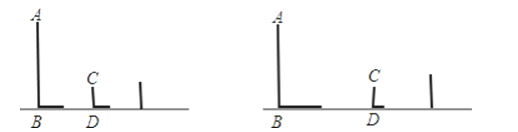
(1)哪个图反映了太阳光下的情形?哪个图反映了路灯下的情形?
(2)在太阳光下,已知小明的身高是1.8米,影长是1.2米,旗杆的影长是4米,求旗杆的高;
(3)请在图中分别画出表示第三根木棒的影长的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
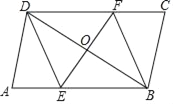
【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
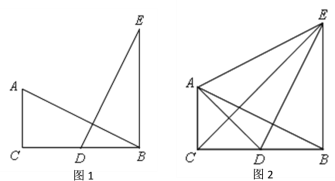
【题目】如图1,在△ABC中,∠ACB=90°,AC=![]() BC,点D为BC的中点,AB =DE,BE∥AC.
BC,点D为BC的中点,AB =DE,BE∥AC.
(1)求证:△ABC≌△DEB;
(2)连结AD、AE、CE,如图2.
①求证:CE是∠ACB的角平分线;
②请判断△ABE是什么特殊形状的三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
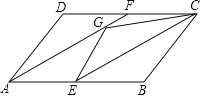
【题目】在ABCD中,点E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G处,连接AG并延长,交CD于F.
(1)求证:四边形AECF是平行四边形;
(2)若CF=5,△GCE的周长为20,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.
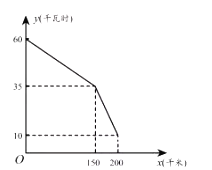
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com