
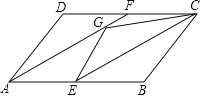
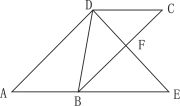
【题目】在ABCD中,点E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G处,连接AG并延长,交CD于F.
(1)求证:四边形AECF是平行四边形;
(2)若CF=5,△GCE的周长为20,求四边形ABCF的周长.
【答案】(1)见解析;(2)30
【解析】
(1)由平行四边形的性质得出AE∥FC,再由三角形的外角的性质,以及折叠的性质,可以证明∠FAE=∠CEB,进而证明AF∥EC,即可得出结论;
(2)由折叠的性质得:GE=BE,GC=BC,由△GCE的周长得出GE+CE+GC=20,BE+CE+BC=20,由平行四边形的性质得出AF=CE,AE=CF=5,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥FC,
∵点E是AB边的中点,
∴AE=BE,
∵将△BCE沿着CE翻折,点B落在点G处,
∴BE=GE,∠CEB=∠CEG,
∴AE=GE,
∴∠FAE=∠AGE,
∵∠CEB=∠CEG=![]() ∠BEG,∠BEG=∠FAE+∠AGE,
∠BEG,∠BEG=∠FAE+∠AGE,
∴∠FAE=![]() ∠BEG,
∠BEG,
∴∠FAE=∠CEB,
∴AF∥EC,
∴四边形AECF是平行四边形;
(2)解:由折叠的性质得:GE=BE,GC=BC,
∵△GCE的周长为20,
∴GE+CE+GC=20,
∴BE+CE+BC=20,
∵四边形AECF是平行四边形,
∴AF=CE,AE=CF=5,
∴四边形ABCF的周长=AB+BC+CF+AF=AE+BE+BC+CE+CF=5+20+5=30.


科目:初中数学 来源: 题型:
【题目】如图,重庆某广场新建与建筑物![]() 垂直的空中玻璃走廊
垂直的空中玻璃走廊![]() 与
与![]() 相连,
相连,![]() 与地面
与地面![]() 垂直.在
垂直.在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() ,测得建筑物
,测得建筑物![]() 处的仰角为
处的仰角为![]() (不计测量人员的身高),
(不计测量人员的身高),![]() 为
为![]() 米.图中的点
米.图中的点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 及直线
及直线![]() 均在同一平面内.
均在同一平面内.
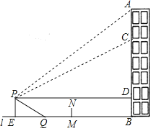
![]() 求
求![]() 、
、![]() 两点的高度差(结果精确到
两点的高度差(结果精确到![]() 米);
米);
![]() 为方便游客,广场从地面
为方便游客,广场从地面![]() 上的
上的![]() 点新建扶梯
点新建扶梯![]() ,
,![]() 所在斜面的坡度
所在斜面的坡度![]() ,
,![]() 到地面
到地面![]() 的距离
的距离![]() 为
为![]() 米.一广告牌
米.一广告牌![]() 位于
位于![]() 的中点
的中点![]() 处,市政规划要求在点
处,市政规划要求在点![]() 右侧需留出
右侧需留出![]() 米的行车道,请判断是否需要挪走广告牌
米的行车道,请判断是否需要挪走广告牌![]() ,并说明理由.(参考数据:
,并说明理由.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
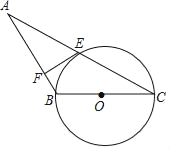
【题目】如图所示,在△ABC中,AB=CB,以BC为直径的⊙O交AC于点E,过点E作⊙O的切线交AB于点F.
(1)求证:EF⊥AB;
(2)若AC=16,⊙O的半径是5,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一组数据![]() ,
,![]() ,
,![]() 中,各数据与它们的平均数
中,各数据与它们的平均数![]() 的差的绝对值的平均数,记作
的差的绝对值的平均数,记作![]() 叫做这组数据的“平均差”.一组数据的平均差越大,就说明这组数据的离散程度越大.则样本:
叫做这组数据的“平均差”.一组数据的平均差越大,就说明这组数据的离散程度越大.则样本:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的平均差是( )
的平均差是( )
A. ![]() B. 3 C. 6 D.
B. 3 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生体能情况,规定参加测试的每名学生从“立定跳远”,“耐久跑”,“掷实心球”,“引体向上”四个项目中随机抽取两项作为测试项目.
(1)小明同学恰好抽到“立定跳远”,“耐久跑”两项的概率是 ;
(2)据统计,初三(3)班共12名男生参加了“立定跳远”的测试,他们的分数如下:95、100、90、82、90、65、89、74、75、93、 92、85.
①这组数据的众数是 ,中位数是 ;
②若将不低于90分的成绩评为优秀,请你估计初三年级参加“立定跳远”的400名男生中成绩为优秀的学生约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
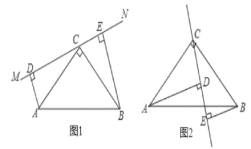
(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由;
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由;
(3)小亮将直线MN绕点C旋转到图2的位置,发现DE、AD、BE之间存在着一个新的数量关系,请直接写出这一数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com