
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
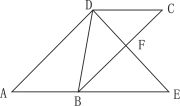
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
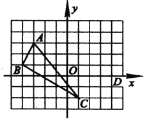
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标: A′(_____,______); B′(_____,______); C′(_____,______)。
(3)求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
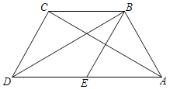
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形的边长都是1,三角形ABC三个顶点与方格纸中小正方形的顶点重合,请在方格纸中分别画出符合要求的图形,具体要求如下:
(1)在图①中平移三角形ABC,点A移动到点P,画出平移后的三角形PMN;
(2)在图②中将三角形ABC三个顶点的横、纵坐标都减去2,画出得到的三角形A1B1C1;
(3)在图③中建立适当的平面直角坐标系,且A点的坐标为(0,2),C点的坐标为(1,5).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D与点E分别是△ABC的边长BC、AC的中点,△ABC的面积是20cm![]() .
.

(1)求△ABD与△BEC的面积;
(2)△AOE与△BOD的面积相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把1240吨甲种货物和880吨乙种货物用一列火车运往某地,已知这列火车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,B型车厢每节费用8000元.如果每节A型车厢最多可装35吨甲种货物和15吨乙种货物,每节B型车厢最多可装25吨甲种货物和35吨乙种货物;
(1)那么共有哪几种安排车厢的方案?
(2)在上述方案中,哪种方案运费最省、最少运费为多少元?
(3)在(1)问下,若两种货物全部售出,且每吨货物售出获利200元,除去运费获
利154000元,问:在这种情况下是按哪种方案安排车厢的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银泰百货名创优品店购进600个钥匙扣,进价为每个8元,第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低![]() 元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景:
我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
已知:如图1,在![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

求证:![]()
问题中既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一线段长的一半.所以可以用“倍长法”将![]() 延长一倍:延长
延长一倍:延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 这样只需证明
这样只需证明![]() ,且
,且![]() .由于
.由于![]() 是
是![]() 的中点,容易证明四边形
的中点,容易证明四边形![]() 、四边形
、四边形![]() 是平行四边形,证明...
是平行四边形,证明...
问题解决:
![]() 上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
A.数形结合思想 B.转化思想 C.分类讨论思想 D.方程思想
![]() 证明四边形
证明四边形![]() 是平行四边形的依据是
是平行四边形的依据是

反思交流:
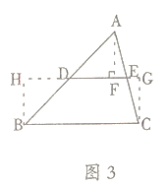
“智慧小组”在证明中位线定理时,在图1的基础上追加了如上辅助线作法:如图3,分别过点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,..
,..
![]() 请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
方法迁移:
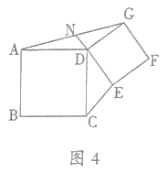
![]() 如图4、四边形
如图4、四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是
是![]() 的中点.求证:
的中点.求证: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com