
【题目】如图,在等腰![]() 中,
中,![]() ,
,![]() 是斜边
是斜边![]() 的中点,
的中点,![]() 交边
交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,连结
,连结![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的面积是( )
的面积是( )
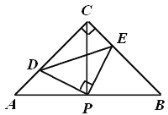
A.2B.2.5C.3D.3.5
【答案】B
【解析】
首先根据等腰直角三角形的性质和余角的性质可证明△BPE≌△CPD,可得PE=PD,于是所求的![]() 的面积即为
的面积即为![]() ,故只要求出PE2的值即可,可过点E作EF⊥AB于点F,如图,根据题意可依次求出BE、BF、BP、PF的长,即可根据勾股定理求出PE2的值,进而可得答案.
,故只要求出PE2的值即可,可过点E作EF⊥AB于点F,如图,根据题意可依次求出BE、BF、BP、PF的长,即可根据勾股定理求出PE2的值,进而可得答案.
解:在![]() 中,∵
中,∵![]() ,AC=BC,
,AC=BC,![]() 是斜边
是斜边![]() 的中点,
的中点,
∴AP=BP=CP,CP⊥AB,∠B=∠BCP=∠DCP=45°,
∵∠DPC+∠EPC=90°,∠BPE+∠EPC=90°,∴∠DPC=∠BPE,
在△BPE和△CPD中,∵∠B=∠DCP,BP=CP,∠BPE=∠DPC,∴△BPE≌△CPD(ASA),
∴PE=PD,
∵![]() ,
,![]() ,∴CE=1,BE=3,
,∴CE=1,BE=3,
过点E作EF⊥AB于点F,如图,则EF=BF=![]() ,
,
又∵BP=![]() ,∴
,∴![]() ,
,
在直角△PEF中,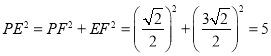 ,
,
∴![]() 的面积=
的面积=![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.等腰三角形的中线与高线重合
C.三边长为![]() 的三角形为直角三角形
的三角形为直角三角形
D.到线段两端距离相等的点在这条线段的垂直平分线上
查看答案和解析>>
科目:初中数学 来源: 题型:
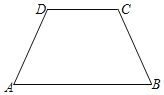
【题目】如图,在四边形ABCD中,AB∥DC,边AD与BC不平行
(1)若∠A=∠B,求证:AD=BC.
(2)已知AD=BC,∠A=70°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
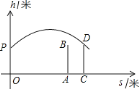
【题目】甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为![]() ,羽毛球距地面高度
,羽毛球距地面高度![]() (米)与其飞行的水平距离
(米)与其飞行的水平距离![]() (米)之间的关系式为
(米)之间的关系式为![]() .如图,已知球网
.如图,已知球网![]() 距原点
距原点![]() 米,乙(用线段
米,乙(用线段![]() 表示)扣球的最大高度为
表示)扣球的最大高度为![]() 米,设乙的起跳点
米,设乙的起跳点![]() 的横坐标为
的横坐标为![]() ,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则
,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则![]() 的取值范围是( )
的取值范围是( )
A. .![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
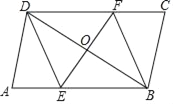
【题目】如图所示,平行四边形形ABCD中,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)请添加一个条件使四边形BEDF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如图9的两幅尚不完整的统计图.
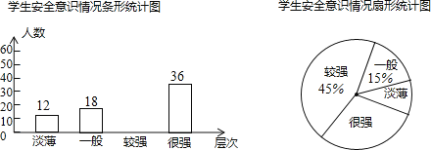
根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生;
(2)请将条形统计图补充完整;
(3)分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com