
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃН2ЃЌЁЯBЃНЁЯCЃН40ЁуЃЌЕуDдкЯпЖЮBCЩЯдЫЖЏЃЈDВЛгыBЁЂCжиКЯЃЉЃЌСЌНгADЃЌзїЁЯADEЃН40ЁуЃЌDEНЛЯпЖЮACгкEЃЎ
ЃЈ1ЃЉЕБЁЯBDAЃН115ЁуЪБЃЌЁЯEDCЃНЁЁ ЁЁЁуЃЌЁЯDECЃНЁЁ ЁЁЁуЃЛЕуDДгBЯђCдЫЖЏЪБЃЌЁЯBDAж№НЅБфЁЁ ЁЁЃЈЬюЁАДѓЁБЛђЁАаЁЁБЃЉЃЛ
ЃЈ2ЃЉЕБDCЕШгкЖрЩйЪБЃЌЁїABDЁеЁїDCEЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЕуDЕФдЫЖЏЙ§ГЬжаЃЌЁїADEЕФаЮзДПЩвдЪЧЕШбќШ§НЧаЮТ№ЃПШєПЩвдЃЌЧыжБНгаДГіЁЯBDAЕФЖШЪ§ЃЎШєВЛПЩвдЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ25ЁуЃЌ115ЁуЃЌаЁЃЛЃЈ2ЃЉЕБDCЃН2ЪБЃЌЁїABDЁеЁїDCEЃЌМћНтЮіЃЛЃЈ3ЃЉЕБЁЯBDAЕФЖШЪ§ЮЊ110ЁуЛђ80ЁуЪБЃЌЁїADEЕФаЮзДЪЧЕШбќШ§НЧаЮЃЌМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁЯBDAЃН115ЁувдМАЁЯADEЃН40ЁуЃЌМДПЩЕУГіЁЯEDCЃН180ЁуЉЁЯADBЉЁЯADEЃЌНјЖјЧѓГіЁЯDECЕФЖШЪ§ЃЌ
ЃЈ2ЃЉЕБDCЃН2ЪБЃЌРћгУЁЯDEC+ЁЯEDCЃН140ЁуЃЌЁЯADB+ЁЯEDCЃН140ЁуЃЌЧѓГіЁЯADBЃНЁЯDECЃЌдйРћгУABЃНDCЃН2ЃЌМДПЩЕУГіЁїABDЁеЁїDCEЃЌ
ЃЈ3ЃЉЕБЁЯBDAЕФЖШЪ§ЮЊ110ЁуЛђ80ЁуЪБЃЌЁїADEЕФаЮзДЪЧЕШбќШ§НЧаЮЃЎ
НтЃКЃЈ1ЃЉЁЯEDCЃН180ЁуЉЁЯADBЉЁЯADEЃН180ЁуЉ115ЁуЉ40ЁуЃН25ЁуЃЌ
ЁЯDECЃН180ЁуЉЁЯEDCЉЁЯCЃН180ЁуЉ40ЁуЉ25ЁуЃН115ЁуЃЌ
ЁЯBDAж№НЅБфаЁЃЛ
ЙЪД№АИЮЊЃК25ЁуЃЌ115ЁуЃЌаЁЃЛ
ЃЈ2ЃЉЕБDCЃН2ЪБЃЌЁїABDЁеЁїDCEЃЌ
РэгЩЃКЁпЁЯCЃН40ЁуЃЌ
ЁрЁЯDEC+ЁЯEDCЃН140ЁуЃЌ
гжЁпЁЯADEЃН40ЁуЃЌ
ЁрЁЯADB+ЁЯEDCЃН140ЁуЃЌ
ЁрЁЯADBЃНЁЯDECЃЌ
гжЁпABЃНDCЃН2ЃЌ
ЁрЁїABDЁеЁїDCEЃЈAASЃЉЃЌ
ЃЈ3ЃЉЕБЁЯBDAЕФЖШЪ§ЮЊ110ЁуЛђ80ЁуЪБЃЌЁїADEЕФаЮзДЪЧЕШбќШ§НЧаЮЃЌ
РэгЩЃКЁпЁЯBDAЃН110ЁуЪБЃЌ
ЁрЁЯADCЃН70ЁуЃЌ
ЁпЁЯCЃН40ЁуЃЌ
ЁрЁЯDACЃН70ЁуЃЌЁЯAEDЃНЁЯC+ЁЯEDCЃН30Ёу+40ЁуЃН70ЁуЃЌ
ЁрЁЯDACЃНЁЯAEDЃЌ
ЁрЁїADEЕФаЮзДЪЧЕШбќШ§НЧаЮЃЛ
ЁпЕБЁЯBDAЕФЖШЪ§ЮЊ80ЁуЪБЃЌ
ЁрЁЯADCЃН100ЁуЃЌ
ЁпЁЯCЃН40ЁуЃЌ
ЁрЁЯDACЃН40ЁуЃЌ
ЁрЁЯDACЃНЁЯADEЃЌ
ЁрЁїADEЕФаЮзДЪЧЕШбќШ§НЧаЮЃЎ



 ХргХПкЫуЬтПЈЯЕСаД№АИ
ХргХПкЫуЬтПЈЯЕСаД№АИ ПЊаФПкЫуЬтПЈЯЕСаД№АИ
ПЊаФПкЫуЬтПЈЯЕСаД№АИ ПкЫуЬтПЈКгББЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
ПкЫуЬтПЈКгББЩйФъЖљЭЏГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌAHЁЭBCЃЌДЙзуЮЊHЃЌDЮЊжБЯпBCЩЯвЛЖЏЕу(ВЛгыЕуBCжиКЯ)ЃЌдкADЕФгвВрзїЁїADEЃЌЪЙЕУAE=ADЃЌЁЯDAE=ЁЯBACЃЌСЌНгCE.
(1)ЕБDдкЯпЖЮBCЩЯЪБ,ЧѓжЄ:ЁїBADЁеЁїCAEЃЛ
(2)ЕБЕуDдЫЖЏЕНКЮДІЪБЃЌACЁЭDEЃЌВЂЫЕУїРэгЩЃЛ
(3)ЕБCEЁЮABЪБЃЌШєЁїABDжазюаЁНЧЮЊ20ЁуЃЌЪдЬНОПЁЯADBЕФЖШЪ§(жБНгаДГіНсЙћЃЌЮоашаДГіЧѓНтЙ§ГЬ).

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯп![]() гыСНзјБъжсНЛгк
гыСНзјБъжсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌвд
СНЕуЃЌвд![]() ЮЊаББпдкЕкЖўЯѓЯоФкзїЕШбќ
ЮЊаББпдкЕкЖўЯѓЯоФкзїЕШбќ![]() ЃЌ
ЃЌ![]() ЕФЭМЯѓЙ§Еу
ЕФЭМЯѓЙ§Еу![]() ЃЌдђ
ЃЌдђ![]() ________ЃЎ
________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
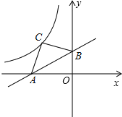
ЁОЬтФПЁПЯТУцЪЧаЁУїЭЌбЇЩшМЦЕФЁАвбжЊЕзБпМАЕзБпЩЯЕФжаЯпзїЕШбќШ§НЧаЮЁБЕФГпЙцзїЭМЙ§ГЬЃЎ

вбжЊЃКШчЭМ 1ЃЌЯпЖЮ a КЭЯпЖЮ bЃЎ
ЧѓзїЃКЁїABCЃЌЪЙЕУ AB = ACЃЌBC = aЃЌBC БпЩЯЕФжаЯпЮЊ bЃЎ
зїЗЈЃКШчЭМ ЃЌ
![]()
Ђй зїЩфЯп BMЃЌВЂдкЩфЯп BM ЩЯНиШЁ BC = aЃЛ
Ђк зїЯпЖЮ BC ЕФДЙжБЦНЗжЯп PQЃЌPQ НЛ BC гк DЃЛ
Ђл вд D ЮЊдВаФЃЌb ЮЊАыОЖзїЛЁЃЌНЛ PQ гк AЃЛ
Ђм СЌНг AB КЭ ACЃЎ
дђЁїABC ЮЊЫљЧѓзїЕФЭМаЮЃЎ
ИљОнЩЯЪізїЭМЙ§ГЬЃЌЛиД№ЮЪЬтЃК
ЃЈ1ЃЉгУжБГпКЭдВЙцЃЌВЙШЋЭМ 2 жаЕФЭМаЮЃЛ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃК
жЄУїЃКгЩзїЭМПЩжЊ BC = aЃЌAD = bЃЎ
Ёп PQ ЮЊЯпЖЮ BC ЕФДЙжБЦНЗжЯпЃЌЕу A дк PQ ЩЯЃЌ
Ёр AB = ACЃЈ ЃЉЃЈЬювРОнЃЉЃЎ
гжЁпЯпЖЮ BC ЕФДЙжБЦНЗжЯп PQ НЛ BC гк DЃЌ
Ёр BD=CDЃЎЃЈ ЃЉЃЈЬювРОнЃЉЃЎ
Ёр AD ЮЊ BC БпЩЯЕФжаЯпЃЌЧв AD = bЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
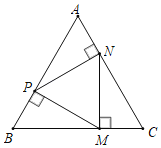
ЁОЬтФПЁПШчЭМЃЌЕуPЃЌMЃЌNЗжБ№дкЕШБпЁїABCЕФИїБпЩЯЃЌЧвMPЁЭABгкЕуPЃЌMNЁЭBCгкЕуMЃЌPNЁЭACгкЕуNЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїPMNЪЧЕШБпШ§НЧаЮЃЛ
ЃЈ2ЃЉШєABЃН18cmЃЌЧѓCMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮхвЛЦкМфЃЌаЁУївЛМввЛЦ№ШЅТУгЮЃЌШчЭМЪЧаЁУїЩшМЦЕФФГТУгЮОАЕуЕФЭМжН(ЭјИёЪЧгЩЯрЭЌЕФаЁе§ЗНаЮзщГЩЕФЃЌЧваЁе§ЗНаЮЕФБпГЄДњБэЪЕМЪГЄЖШ100m)ЃЌдкИУЭМжНЩЯПЩПДЕНСНИіБъжОадОАЕуAЃЌB.ШєНЈСЂЪЪЕБЕФЦНУцжБНЧзјБъЯЕЃЌдђЕуA(Ѓ3ЃЌ1)ЃЌB(Ѓ3ЃЌЃ3)ЃЌЕкШ§ИіОАЕуC(3ЃЌ2)ЕФЮЛжУвбЦЦЫ№ЃЎ
(1)ЧыдкЭМжаБъГіОАЕуCЕФЮЛжУЃЛ
(2)аЁУїЯыДгОАЕуBПЊЪМгЮЭцЃЌЭОООАЕуAЃЌзюКѓЕНДяОАЕуCЃЌЧѓаЁУївЛМвзюЖЬЕФаазпТЗГЬ(ВЮПМЪ§ОнЃК![]() Ёж6ЃЌНсЙћБЃСєећЪ§)ЃЎ
Ёж6ЃЌНсЙћБЃСєећЪ§)ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ![]() ЗжБ№ЪЧЯпЖЮ
ЗжБ№ЪЧЯпЖЮ![]() ЃЌ
ЃЌ![]() ЩЯЕФЕуЃЌСЌНг
ЩЯЕФЕуЃЌСЌНг![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌШєЕу
ЮЊе§ЗНаЮЃЌШєЕу![]() ЪЧ
ЪЧ![]() ЩЯЕФЖЏЕуЃЌСЌНг
ЩЯЕФЖЏЕуЃЌСЌНг![]() ЃЌНЋОиаЮби
ЃЌНЋОиаЮби![]() елЕўЪЙЕУЕу
елЕўЪЙЕУЕу![]() Тфдке§ЗНаЮ
Тфдке§ЗНаЮ![]() ЕФЖдНЧЯпЫљдкЕФжБЯпЩЯЃЌЖдгІЕуЮЊ
ЕФЖдНЧЯпЫљдкЕФжБЯпЩЯЃЌЖдгІЕуЮЊ![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ЕФГЄЮЊ________ЃЎ
ЕФГЄЮЊ________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЊНЈвЛИіШчЭМЫљЪОЕФУцЛ§ЮЊ300![]() ЕФГЄЗНаЮЮЇРИЃЌЮЇРИзмГЄ50mЃЌвЛБпППЧНЃЈЧНГЄ25mЃЉЃЌ
ЕФГЄЗНаЮЮЇРИЃЌЮЇРИзмГЄ50mЃЌвЛБпППЧНЃЈЧНГЄ25mЃЉЃЌ

ЃЈ1ЃЉЧѓЮЇРИЕФГЄКЭПэЃЛ
ЃЈ2ЃЉФмЗёЮЇГЩУцЛ§ЮЊ400 ![]() ЕФГЄЗНаЮЮЇРИЃПШчЙћФмЃЌЧѓГіИУГЄЗНаЮЕФГЄКЭПэЃЌШчЙћВЛФмЧыЫЕУїРэгЩЁЃ
ЕФГЄЗНаЮЮЇРИЃПШчЙћФмЃЌЧѓГіИУГЄЗНаЮЕФГЄКЭПэЃЌШчЙћВЛФмЧыЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃН2x2Љ8x+mТњзувдЯТЬѕМўЃКЕБЉ2ЃМxЃМЉ1ЪБЃЌЫќЕФЭМЯѓЮЛгкxжсЕФЯТЗНЃЛЕБ6ЃМxЃМ7ЪБЃЌЫќЕФЭМЯѓЮЛгкxжсЕФЩЯЗНЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. 8 B. Љ10 C. Љ42 D. Љ24
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com