
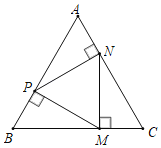
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=18cm,求CM的长.
【答案】(1)证明见解析;(2)6
【解析】
(1)根据等边三角形的性质得出∠A=∠B=∠C,进而得出∠MPB=∠NMC=∠PNA=90°,再根据平角的意义即可得出∠NPM=∠PMN=∠MNP,即可证得△PMN是等边三角形;
(2)易证得△PBM≌△MCN≌△NAP,得出PA=BM=CN,PB=MC=AN,从而求得BM+PB=AB=12cm,根据直角三角形30°角所对的直角边等于斜边的一半得出2PB=BM,即可求得PB的长,进而得出CM的长.
(1)证明:∵△ABC是正三角形,
∴∠A=∠B=∠C,
∵MP⊥AB,MN⊥BC,PN⊥AC,
∴∠MPB=∠NMC=∠PNA=90°,
∴∠PMB=∠MNC=∠APN,
∴∠NPM=∠PMN=∠MNP,
∴△PMN是等边三角形;
(2)解:∵△PMN是等边三角形,
∴PM=MN=NP,
在△PBM、△MCN和△NAP中,
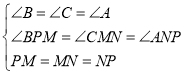 ,
,
∴△PBM≌△MCN≌△NAP(AAS),
∴PA=BM=CN,PB=CM=AN,
∴BM+PB=AB=18cm,
∵△ABC是正三角形,
∴∠A=∠B=∠C=60°,
∴2PB=BM,
∴2PB+PB=18cm,
∴PB=6cm,
∴CM=6cm.


科目:初中数学 来源: 题型:
【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
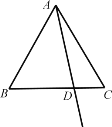
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两名同学在同一个学校上学,B同学上学的路上经过A同学家。A同学步行,B同学骑自行车,某天,A,B两名同学同时从家出发到学校,如图,![]() A表示A同学离B同学家的路程
A表示A同学离B同学家的路程![]() A(m)与行走时间
A(m)与行走时间![]() (min)之间的函数关系图象,
(min)之间的函数关系图象,![]() B表示B同学离家的路程
B表示B同学离家的路程![]() B(m)与行走时间
B(m)与行走时间![]() (min)之间的函数关系图象.
(min)之间的函数关系图象.
(1)A,B两名同学的家相距________m.
(2)B同学走了一段路后,自行车发生故障,进行修理,修理自行车所用的时间是 _____min.
(3)B同学出发后______min与A同学相遇.
(4)求出A同学离B同学家的路程![]() A与时间
A与时间![]() 的函数关系式.
的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整,原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若![]() =3,求
=3,求![]() 的值.
的值.

(1)尝试探究:
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是________,
CG和EH的数量关系是________,
![]() 的值是________.
的值是________.
(2)类比延伸:
如图2,在原题条件下,若![]() =m(m>0)则
=m(m>0)则![]() 的值是________(用含有m的代数式表示),试写出解答过程.
的值是________(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移:
如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F,若![]() =a,
=a,![]() =b(a>0,b>0)则
=b(a>0,b>0)则![]() 的值是________(用含a、b的代数式表示).
的值是________(用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com