
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

【答案】2![]()
![]() ﹣1
﹣1
【解析】
连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,当点![]() 三点在同一条直线上时,线段FG的长度有最小值,根据
三点在同一条直线上时,线段FG的长度有最小值,根据![]() 求解即可.
求解即可.
连接AC,AG,

∵GO⊥AB,
∴O为AB的中点,即![]()
∵G(0,1),即OG=1,
∴在Rt△AOG中,根据勾股定理得:![]()
∴![]()
又CO=CG+GO=2+1=3,
∴在Rt△AOC中,根据勾股定理得:![]()
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
AC的中点为![]()
当点![]() 三点在同一条直线上时,线段FG的长度有最小值,
三点在同一条直线上时,线段FG的长度有最小值,
![]()
![]()
![]()
![]()
故答案为:(1). 2![]() (2).
(2). ![]() ﹣1
﹣1


科目:初中数学 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
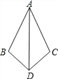
A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.点D,E分别在AB,AC边上,点F在AC边的延长线上,且BD=CE=CF.
(1)连接DE,判断DE与BC的位置关系,为什么?
(2)连接DF交BC于点G.判断DG与GF的数量关系,并说明理由.
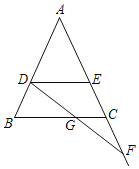
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).
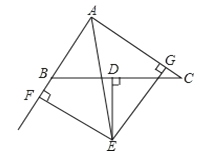
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程.

已知:如图 1,线段 a 和线段 b.
求作:△ABC,使得 AB = AC,BC = a,BC 边上的中线为 b.
作法:如图 ,
![]()
① 作射线 BM,并在射线 BM 上截取 BC = a;
② 作线段 BC 的垂直平分线 PQ,PQ 交 BC 于 D;
③ 以 D 为圆心,b 为半径作弧,交 PQ 于 A;
④ 连接 AB 和 AC.
则△ABC 为所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图 2 中的图形;
(2)完成下面的证明:
证明:由作图可知 BC = a,AD = b.
∵ PQ 为线段 BC 的垂直平分线,点 A 在 PQ 上,
∴ AB = AC( )(填依据).
又∵线段 BC 的垂直平分线 PQ 交 BC 于 D,
∴ BD=CD.( )(填依据).
∴ AD 为 BC 边上的中线,且 AD = b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=18cm,求CM的长.
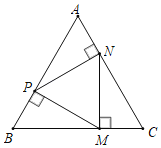
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班为了配合学校体育文化月活动的开展,同学们从捐助的班费中拿出一部分钱来购买羽毛球拍和跳绳。已知购买一副羽毛球拍比购买一根跳绳多20元。若用200元购买羽毛球拍和用80元购买跳绳,则购买羽毛球拍的副数是购买跳绳根数的一半。
(1)求购买一副羽毛球拍、一根跳绳各需多少元?
(2)双11期间,商店老板给予优惠,购买一副羽毛球拍赠送一根跳绳,如果八(1)班需要的跳绳根数比羽毛球拍的副数的![]() 倍还多
倍还多![]() ,且该班购买羽毛球拍和跳绳的总费用不超过
,且该班购买羽毛球拍和跳绳的总费用不超过![]() 元,那么八(1)班最多可购买多少副羽毛球拍?
元,那么八(1)班最多可购买多少副羽毛球拍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com