
【题目】直线![]() 与两坐标轴交于
与两坐标轴交于![]() 、
、![]() 两点,以
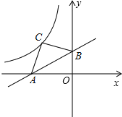
两点,以![]() 为斜边在第二象限内作等腰
为斜边在第二象限内作等腰![]() ,
,![]() 的图象过点
的图象过点![]() ,则
,则![]() ________.
________.
【答案】-9
【解析】
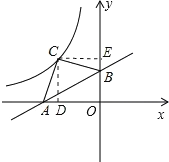
过C点作CD⊥x轴于D,CE⊥y轴于E,先确定A点坐标为(4,0),B点坐标为(0,2),再利用勾股定理计算出AB=2![]() ,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB=
,然后根据等腰三角形的性质得到∠ACB=90°,CA=CB=![]() AB=
AB=![]() ,由于∠DCE=90°,根据等角的余角相等得到∠ACD=∠BCE,易证得Rt△ACD≌Rt△BCE,则CD=CE,得到四边形CDOE为正方形,并且正方形CDOE的面积=四边形CAOB的面积,再计算出四边形CAOB的面积=S△CAB+S△OAB=
,由于∠DCE=90°,根据等角的余角相等得到∠ACD=∠BCE,易证得Rt△ACD≌Rt△BCE,则CD=CE,得到四边形CDOE为正方形,并且正方形CDOE的面积=四边形CAOB的面积,再计算出四边形CAOB的面积=S△CAB+S△OAB=![]() CACB+
CACB+![]() OAOB=9,则CD=CE=3,可确定C点坐标为(3,3),然后把C点坐标代入反比例函数解析式即可得到k的值.
OAOB=9,则CD=CE=3,可确定C点坐标为(3,3),然后把C点坐标代入反比例函数解析式即可得到k的值.
如图,过C点作CD⊥x轴于D,CE⊥y轴于E,
令x=0,y=2;令y=0,
![]() x+2=0,解得x=4,则A点坐标为(4,0),B点坐标为(0,2),
x+2=0,解得x=4,则A点坐标为(4,0),B点坐标为(0,2),
在Rt△OAB中,OA=4,OB=2,
![]() ,
,
∵△ACB为等腰直角三角形,
∴∠ACB=90°,CA=CB=![]() AB=
AB=![]() ,
,
而∠DCE=90°,
∴∠ACD=∠BCE,
∴Rt△ACD≌Rt△BCE,
∴CD=CE,
∴四边形CDOE为正方形,
∴正方形CDOE的面积=四边形CAOB的面积=S△CAB+S△OAB=![]() CACB+
CACB+![]() OAOB=
OAOB=![]()
![]() ×
×![]() +
+![]() ×4×2=9,
×4×2=9,
∴CD=CE=3,
∴C点坐标为(3,3),
把C(3,3)代入y=![]() 得k=3×3=9.
得k=3×3=9.
故答案为:9.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,过点A(2,0)的两条直线![]() ,
,![]() 分别交
分别交![]() 轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=
轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.

(1)求点B的坐标;
(2)若△ABC的面积为4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.

(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△ONC的面积是△OAC面积的![]() 时,求出这时点N的坐标.
时,求出这时点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com