
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为______.

【答案】(﹣![]() ,
,![]() )
)
【解析】
首先过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=x,那么CE=3﹣x,DE=x,利用勾股定理即可求出OE的长度,而利用已知条件可以证明△AEO∽△ADF,而AD=AB=3,接着利用相似三角形的性质即可求出DF、AF的长度,也就求出了D的坐标.
解:如图,过D作DF⊥AO于F,
∵点B的坐标为(1,3),
∴BC=AO=1,AB=OC=3,
根据折叠可知:CD=BC=OA=1,∠CDE=∠B=∠AOE=90°,AD=AB=3,
在△CDE和△AOE中,
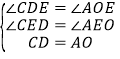 ,
,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,AE=CE,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3﹣x)2=x2+12,
∴x=![]() ,
,
∴OE=![]() ,AE=CE=OC﹣OE=3﹣
,AE=CE=OC﹣OE=3﹣![]() =
=![]() ,
,
又∵DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
∴AE:AD=EO:DF=AO:AF,
即![]() :3=
:3=![]() :DF=1:AF,
:DF=1:AF,
∴DF=![]() ,AF=
,AF=![]() ,
,
∴OF=![]() ﹣1=
﹣1=![]() ,
,
∴D的坐标为:(﹣![]() ,
,![]() ).
).
故答案为:(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
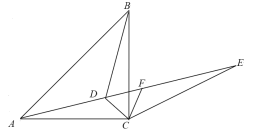
【题目】如图,已知在△ABC中,∠ACB=90°,AC=BC,∠CAD=∠CBD.
(1)求证:CD平分∠ACB;
(2)点E是AD延长线上一点,CE=CA,CF∥BD交AE于点F,若∠CAD=15°,
求证:EF=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
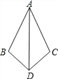
A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点BC重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果,无需写出求解过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在∠MON的角平分线上,过点P作OP的垂线交OM,ON于C、D,PA⊥OM.PB⊥ON,垂足分别为A、B,EP∥BD,则下列结论错误的是( )
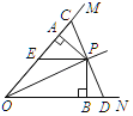
A.CP=PDB.PA=PBC.PE=OED.OB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.点D,E分别在AB,AC边上,点F在AC边的延长线上,且BD=CE=CF.
(1)连接DE,判断DE与BC的位置关系,为什么?
(2)连接DF交BC于点G.判断DG与GF的数量关系,并说明理由.
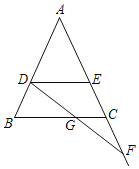
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com