
����Ŀ����2016���������У���֪���������ε����߳�������������������
��ϣ���ļ���ѧ�Һ������������⣬�����������������ۡ�һ���и����˼��㹫ʽ��������ʽS=![]() ������a��b��c�������ε����߳���p=
������a��b��c�������ε����߳���p=![]() ��SΪ�����ε����������������֤��
��SΪ�����ε����������������֤��
���磺����ABC�У�a=3��b=4��c=5����ô������������������㣺
��a=3��b=4��c=5����p=![]() =6����S=
=6����S=![]() =
=![]() =6��
=6��
��ʵ�ϣ�������֪�����ε����߳�����������������⣬�������ҹ�����ʱ����ѧ���ؾ���������ؾ��ع�ʽ�ȷ��������
��ͼ������ABC�У�BC=5��AC=6��AB=9
��1���ú���ʽ����ABC�������
��2������ABC������Բ�뾶r��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() �ֱ���ֱ��
�ֱ���ֱ��![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �Ľ�ƽ�����ཻ�ڵ�
�Ľ�ƽ�����ཻ�ڵ�![]() ������
������![]() Ϊֱ����
Ϊֱ����![]() �����
�����![]() ��
��![]() ��λ�ù�ϵ�ǣ� ��
��λ�ù�ϵ�ǣ� ��

A. ��P�ڡ�O�� B. ��P�ڡ�O��
C. ��P�ڡ�O�� D. ���϶��п���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ڡ�MON�Ľ�ƽ�����ϣ�����P��OP�Ĵ��߽�OM��ON��C��D��PA��OM��PB��ON������ֱ�ΪA��B��EP��BD�������н��۴�����ǣ�������
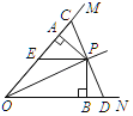
A.CP��PDB.PA��PBC.PE��OED.OB��CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����D��E�ֱ���AB��AC���ϣ���F��AC�ߵ��ӳ����ϣ���BD��CE��CF��
��1������DE���ж�DE��BC��λ�ù�ϵ��Ϊʲô��
��2������DF��BC�ڵ�G���ж�DG��GF��������ϵ����˵�����ɣ�
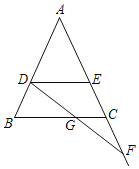
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��![]() ���������ύ��
���������ύ��![]() ��
��![]() ���㣬��
���㣬��![]() Ϊб���ڵڶ�������������
Ϊб���ڵڶ�������������![]() ��
��![]() ��ͼ�����
��ͼ�����![]() ����
����![]() ________��
________��
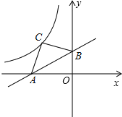
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC��BC���ϵĴ�ֱƽ����DE����BAC��ƽ���߽��ڵ�E��EF��AB��AB���ӳ����ڵ�F��EG��AC���ڵ�G��
��֤����1��BF=CG����2��AF=![]() ��AB+AC����
��AB+AC����
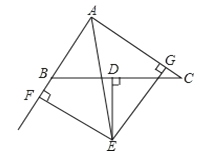
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��M��N�ֱ��ڵȱߡ�ABC�ĸ����ϣ���MP��AB�ڵ�P��MN��BC�ڵ�M��PN��AC�ڵ�N��
��1����֤����PMN�ǵȱ������Σ�
��2����AB��18cm����CM�ij���
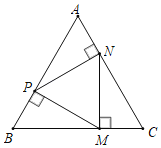
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(-2��4)��B������Ϊ(-4��2)��
(2)��(1)��ǰ���£��ڵڶ������ڵĸ������һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C��������ǣ�
(3)��((2)�С�ABC���ܳ�(�����������)��
(4)����((2)����ABC����y��ԳƵ���A'B'C'.
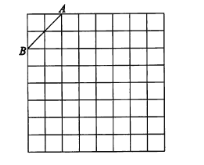
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com