
【题目】用适当方法解下列方程
(1)![]() ;
;
(2)![]()
(3)![]()
(4)![]()
【答案】(1)x1=3,x2=﹣3;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=2,x2=5;(4)x1=4,x2=﹣
;(3)x1=2,x2=5;(4)x1=4,x2=﹣![]()
【解析】
(1)用平方差公式因式分解求出方程的根;(2)用配方法求出方程的根;(3)用提公因式法因式分解求出方程的根;(4)先整理成一般形式,再用公式法求出方程的根.
解:(1)x2-9=0
(x-3)(x+3)=0
x-3=0或x+3=0
∴x1=3,x2=﹣3
(2)![]()
x2+4x+4-7=0
(x+2)2=7
x+2=![]() 或x+2=
或x+2=![]()
∴x1=![]() ,x2=
,x2=![]()
(3)![]()
(x-2)2-3(x-2)=0
(x-2)(x-2-3)=0
x-2=0或x-2-3=0
∴x1=2,x2=5
(4)![]()
整理得:3x2-10x-8=0
a=3,b=-10,c=-8
b2-4ac=(-10)2-4×3×(-8)=196
x=![]()
∴x1=4,x2=﹣![]()


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1)-(3)题
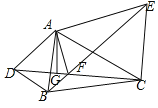
数学课上,老师出示了这样一道题:如图,△ABD和△ACE中,AB=AD,AC=AE,∠DAB=∠CAE=α,连接DC、BE交于点F,过A作AG⊥DC于点G,探究线段FG、FE、FC之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现线段BE与线段DC相等.”
小伟:“通过观察发现,∠AFE与α存在某种数量关系.”
老师:“通过构造全等三角形,从而可以探究出线段FG、FE、FC之间的数量关系.”
(1)求证:BE=CD;
(2)求∠AFE的度数(用含α的式子表示);
(3)探究线段FG、FE、FC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
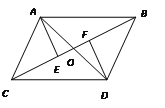
A.5对B.6对C.7对D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西桂林市)已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
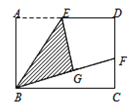
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠 得到△GBE,且点G在矩形ABCD内部.将BG延长交DC 于点F,若DC=nDF,则 ![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
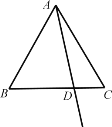
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次夏令营活动中,小明从营地A出发,沿北偏东60°方向走了![]() m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。
m 到达点B,然后再沿北偏西30°方向走了50m到达目的地C。

(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的北偏东多少度方向。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com