
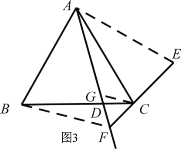
【题目】如图,在等边△ABC 中,点 D 是线段 BC 上一点.作射线 AD ,点 B 关于射线 AD 的对称点为 E .连接 EC 并延长,交射线 AD 于点 F .
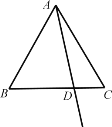
(1)补全图形;(2)求∠AFE 的度数;(3)用等式表示线段 AF 、CF 、 EF 之间的数量关系,并证明.
【答案】(1)答案见解析;(2)60°;(3)AF=EF+CF,理由见解析
【解析】
(1)根据题意补全图形即可;
(2)连接AE,根据对称性得到AE AB , FAB FAE ,设FAC ,则FAB FAE 60 ,故EAC 60 60 2,再根据AE AC 得到AFE 180 FAE FEA 60;
(3)作FCG 60 交 AD 于点 G,连接 BF,根据等边三角形的性质得到ACG 60 GCD BCF,再证明△ ACG ≌△ BCF,得到AG BF,再根据对称性得到BF EF 再得到AF EF CF
(1)补全图形:
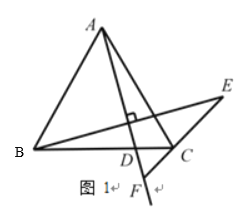
(2)连接AE,
∵△ABC 是等边三角形,
∴ AB AC BC , BAC BCA 60.
∵点B关于射线 AD 的对称点为 E ,
∴ AE AB ,FAB FAE .
设FAC ,则FAB FAE 60
∴ EAC 60 60 2, 又 AE AC .
∴ AFE 180 FAE FEA 60
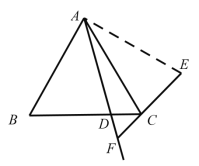
(3) AF EF CF
证明:如图 3,作FCG 60 交 AD 于点 G,连接 BF.
∴△ FCG 是等边三角形.
∴ GF CF GC . CGF GFC FCG 60 .
∴ACG 60 GCD BCF
在△ ACG 和△ BCF 中,
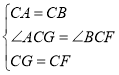
∴△ ACG ≌△ BCF .
∴ AG BF .
∵点 B 关于射线 AD 的对称点为 E ,
∴ BF EF .
∵ AF AG GF .
∴ AF EF CF


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
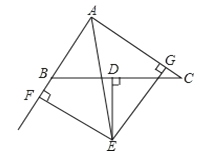
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把形如x2=a(其中a是常数且a≥0)这样的方程叫做x的完全平方方程.
如x2=9,(3x﹣2)2=25,![]() …都是完全平方方程.
…都是完全平方方程.
那么如何求解完全平方方程呢?
探究思路:
我们可以利用“乘方运算”把二次方程转化为一次方程进行求解.
如:解完全平方方程x2=9的思路是:由(+3)2=9,(﹣3)2=9可得x1=3,x2=﹣3.
解决问题:
(1)解方程:(3x﹣2)2=25.
解题思路:我们只要把 3x﹣2 看成一个整体就可以利用乘方运算进一步求解方程了.
解:根据乘方运算,得3x﹣2=5 或 3x﹣2= .
分别解这两个一元一次方程,得x1=![]() ,x2=﹣1.
,x2=﹣1.
(2)解方程![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
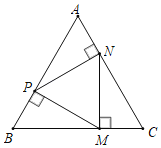
【题目】如图,点P,M,N分别在等边△ABC的各边上,且MP⊥AB于点P,MN⊥BC于点M,PN⊥AC于点N.
(1)求证:△PMN是等边三角形;
(2)若AB=18cm,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD、AE分别是△ABC的中线、高,且AB=4cm,AC=3cm,请解答下列问题:
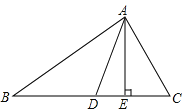
(1)△ABD与△ACD的面积大小有怎样的关系?并说明理由.
(2)△ABD与△ACD的周长之差是多少?
(3)当AE=2.5cm ,BC=6cm时,试求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A、C重合,直线MN交AC于O.

(1)求证:△COM∽△CBA;
(2)求线段OM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
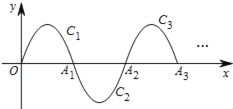
【题目】如图,我们把抛物线y=﹣x(x﹣3)(0≤x≤3)记为C1,它与x轴交于点O,A1将C1绕点A1旋转180°得C2,交x 轴于另一点A2;将C2绕点A2旋转180°得C3,交x 轴于另一点A3;…;如此进行下去,直至得C2016.①C1的对称轴方程是_____;②若点P(6047,m)在抛物线C2016上,则m=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com