
����Ŀ���Ķ�������ϣ���ɣ�1��-��3����
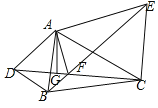
��ѧ���ϣ���ʦ��ʾ������һ���⣺��ͼ����ABD�͡�ACE�У�AB��AD��AC��AE����DAB����CAE����������DC��BE���ڵ�F����A��AG��DC�ڵ�G��̽���߶�FG��FE��FC֮���������ϵ����֤����
ͬѧ�Ǿ���˼�����������ѵ��뷨��
С������ͨ���۲�Ͷ����������߶�BE���߶�DC��ȣ���
Сΰ����ͨ���۲췢�֣���AFE��������ij��������ϵ����
��ʦ����ͨ������ȫ�������Σ��Ӷ�����̽�����߶�FG��FE��FC֮���������ϵ����
��1����֤��BE��CD��
��2�����AFE�Ķ������ú�����ʽ�ӱ�ʾ����
��3��̽���߶�FG��FE��FC֮���������ϵ����֤����
���𰸡���1������������2����AFE��![]() ����3��EF��FC+2GF��������
����3��EF��FC+2GF��������
��������
��1���ɡ�DAB����CAE�������ɵá�DAC����BAE��������SAS����֤��ADC�ա�ABE���ɵ�DC��BE��
��2������ADC�ա�ABE�ɵá�AEF����ACD������֤��A����E����C����F�ĵ㹲Բ���ɵá�AFE����ACE�����ݵ��������ε����ʺ��������ڽǺͶ��������AFE�Ķ�����
��3�����ۣ�EF��FC+2GF��������ɵá�AFD��![]() ����AFE��������AH��BE����֤��AGF�ա�AHF���ɵ�AG��AH��GF��HF������֤Rt��AGC��Rt��AHE���ɵ�GC��HE����EF��FC��2GF�ɵý��ۣ�
����AFE��������AH��BE����֤��AGF�ա�AHF���ɵ�AG��AH��GF��HF������֤Rt��AGC��Rt��AHE���ɵ�GC��HE����EF��FC��2GF�ɵý��ۣ�
֤������1���ߡ�DAB����CAE������
���DAC����BAE����AD��AB��AC��AE
���ADC�ա�ABE��SAS��
��DC��BE��
��2���ߡ�ADC�ա�ABE
���AEF����ACD
���A����E����C����F�ĵ㹲Բ
���AFE����ACE
��AC��AE����DAB����CAE����
���ACE��![]() ��
��
���AFE��![]() ��
��
��3�����ۣ�EF��FC+2GF��
���ɣ��ߡ�ADC�ա�ABE
���ADC����ABE
���A����D����B����F�ĵ㹲Բ
���AFD����ABD
��AB��AD����DAB����CAE����
���ABD��![]() ��
��
���AFD��![]() ��
��
���AFE����AFD
��ͼ��������AH��BE��
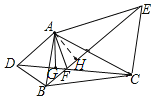
�ߡ�AFE����AFD����AGF����AHF��AF��AF
���AGF�ա�AHF��AAS��
��AG��AH��GF��HF��
��AG��AH��AE��AC
��Rt��AGC��Rt��AHE��HL��
��GC��HE
��EF��FC��HE+FH��FC��GC+FH��FC��GF+FC+FH��FC��2GF��
��EF��FC+2GF��


 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
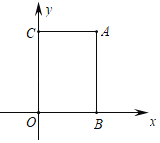
����Ŀ����ͼ��������ABOC�е�A����Ϊ��4��5������E��x����һ���㣬����AE���ѡ�B��AE�۵�������B����y����ʱ��E������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��ֱ��
��ֱ��![]() Ϊ
Ϊ![]() ��
��![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ����
����![]() ��
��![]() ���е㣬��ֱ��
���е㣬��ֱ��![]() ��������
��������![]() ��ʹ
��ʹ![]() ��ֵ��С����
��ֵ��С����![]() ����СֵΪ________��
����СֵΪ________��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x��һԪ���η���ax2+bx+c=0������ʵ������������һ����Ϊ��һ��������������������ķ���Ϊ��3����������������˵������ȷ���ǣ�������
A. ����x2��4x+3=0��3��������
B. ������x�ķ��̣�x��3����mx+n��=0��3�������̣���m+n=0
C. ��m+n=0��m��0�������x�ķ��̣�x��3����mx+n��=0��3��������
D. ��3m+n=0��m��0�������x�ķ���x2+��m��n��x��mn=0��3��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ڡ�MON�Ľ�ƽ�����ϣ�����P��OP�Ĵ��߽�OM��ON��C��D��PA��OM��PB��ON������ֱ�ΪA��B��EP��BD�������н��۴�����ǣ�������
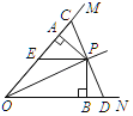
A.CP��PDB.PA��PBC.PE��OED.OB��CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У���E�ڱ�AB�ϣ�����DE��CE��
��1������A=��B=��DEC=50�����ҳ�ͼ�е����������Σ���˵�����ɣ�
��2�����ı���ABCDΪ���Σ�AB=5��BC=2����ͼ�е����������ζ����ƣ���AE�ij���
��3������A=��B=90�㣬AD��BC��ͼ�е����������ζ����ƣ����ж�AE��BE��������ϵ��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD��AE�ֱ�����ABC�����ߡ��ߣ���AB=4cm��AC=3cm�������������⣺
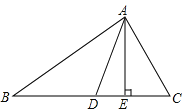
(1)��ABD����ACD�������С�������Ĺ�ϵ����˵������.
(2)��ABD����ACD���ܳ�֮���Ƕ��٣�
(3)��AE=2.5cm ��BC=6cmʱ��������ABD�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com