【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
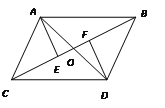
A.5对B.6对C.7对D.8对
【答案】C
【解析】
解：∵AB∥CD，AC∥BD，
∴∠ABC=∠DCB，∠ACB=∠DBC．
∵BC=CB，
∴△CAB≌△CDB，
∴AB=CD，AC=BD．
∵AB∥CD，AC∥BD，
∴∠BAO=∠CDO，∠OBA=∠OCD，∠OBD=∠OCA，∠OAC=∠ODB．
∴△AOB≌△COD，△AOC≌△BOD．
∴OA=OD，OC=OB．
∵AE⊥BC，DF⊥BC，∠AOE=∠DOF，
∴△AOE≌△DOF．
∴OE=OF．
∴CE=BF．
∵AE=DF，AC=BD，
∴△AEC≌△BFD．
∵AE=DF，AB=CD，BE=CF，
∴△AEB≌△DFC．
还有△ACD≌△DBA．
故全等三角形有7对，选：C．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】为响应“学雷锋、树新风、做文明中学生”号召，某校开展了志愿者服务活动，活动项目有“戒毒宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”等五项，活动期间，随机抽取了部分学生对志愿者服务情况进行调查，结果发现，被调查的每名学生都参与了活动，最少的参与了1项，最多的参与了5项，根据调查结果绘制了如图所示不完整的折线统计图和扇形统计图．
（1）被随机抽取的学生共有多少名？
（2）在扇形统计图中，求活动数为3项的学生所对应的扇形圆心角的度数，并补全折线统计图；
（3）该校共有学生2000人，估计其中参与了4项或5项活动的学生共有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，C是⊙O上一点，D在AB的延长线上，且∠BCD=∠A．
（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为3，CD=4，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等．那么在什么情况下，它们会全等？
（1）阅读与证明：
对于这两个三角形均为直角三角形，显然它们全等．
对于这两个三角形均为钝角三角形，可证它们全等（证明略）．
对于这两个三角形均为锐角三角形，它们也全等，可证明如下：
如图所示，
、
均为锐角三角形，
，
，
．
求证：
．
证明：分别过点B，
作
于点D，
于点
．
∴
．
在
和
，
∴
．
．
____________________________________________________________．
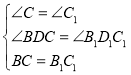
（请你将上述证明过程补充完整）
（2）归纳与叙述：由（1）可得到一个正确结论，请你写出这个结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
中，
厘米，
厘米，点
为
的中点．
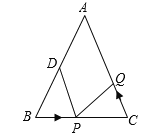
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过1秒后，
与
是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等， 与是否可能全等？若能，求出全等时点Q的运动速度和时间；若不能，请说明理由．
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿三边运动，求经过多长时间点P与点Q第一次在的哪条边上相遇？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在
中，
，
，对角线
，
相交于点
.点
是线段上一动点（不与
、
重合），连接
，以为边在的右侧作
，且
，
.
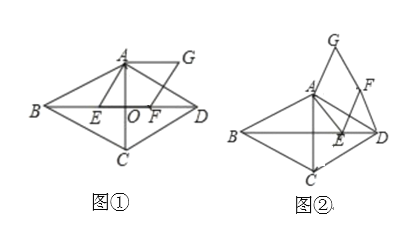
（1）如图①，若点
落在线段上，则线段
与线段
的数量关系是______；
（2）如图②，若点不在线段上，（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，某公司员工住在
三个住宅区，已知
区有2人，
区有7人，
区有12人，三个住宅区在同一条直线上，且
，
是
的中点．为方便员工，公司计划开设通勤车免费接送员工上下班，但因为停车紧张，在
四处只能设一个通勤车停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠站应设在（ ）
A.处B.处C.处D.处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
