
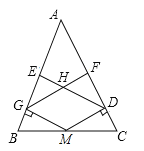
【题目】在△ABC中,AB=AC,BM=CM,MD⊥AC,MG⊥AB,DE⊥AB,GF⊥AC.求证:四边形HGMD是菱形.
科目:初中数学 来源: 题型:
【题目】蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计.以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题: :
组别 | 分组 | 频数 | 频率 |
1 |
| 9 | 0.18 |
2 |
|
|
|
3 |
| 21 | 0.42 |
4 |
|
| 0.06 |
5 |
| 2 |
|

(1)根据上表填空: ![]() __,
__,![]() =. ,
=. ,![]() = .
= .
(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在![]() 的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是直角三角形
是直角三角形![]() 斜边
斜边![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() ,分别过点
,分别过点![]() ,
,![]() 向直线
向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() ,
,![]() ,
,![]() 为斜边
为斜边![]() 的中点.
的中点.
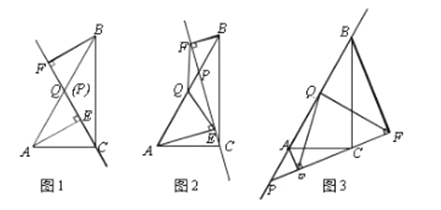
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() 与
与![]() 的位置关系是______,
的位置关系是______,![]() 与
与![]() 的数量关系是______;
的数量关系是______;
(2)如图2,当点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 重合)时,试猜想
重合)时,试猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
的延长线上时,此时(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
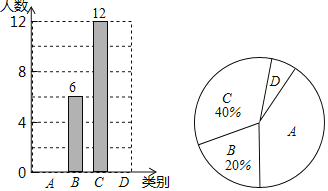
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB∥CD, AC∥BD, AD与BC交于O, AE⊥BC于E, DF⊥BC于F, 那么图中全等的三角形有 ( )
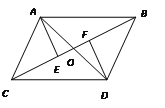
A.5对B.6对C.7对D.8对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2

(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,3),B(5,1),C(1,3),结合所给的平面直角坐标系,解答下列问题: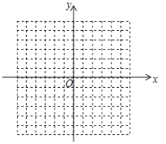
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于x轴对称的△A′B′C′,并写出△A′B′C′各顶点坐标;
(3)在x轴上找一点P,使PA+PB的值最小。请画出点P,并求出点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
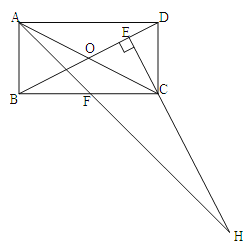
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com