
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
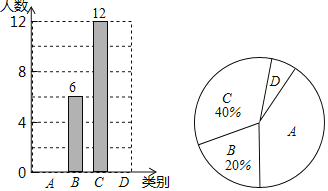
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
【答案】(1)30;(2)①补图见解析;②120;③70人.
【解析】(1)由B类别人数及其所占百分比可得总人数;
(2)①设D类人数为a,则A类人数为5a,根据总人数列方程求得a的值,从而补全图形;
②用360°乘以A类别人数所占比例可得;
③总人数乘以样本中C、D类别人数和所占比例.
(1)本次调查的好友人数为6÷20%=30人,
故答案为:30;
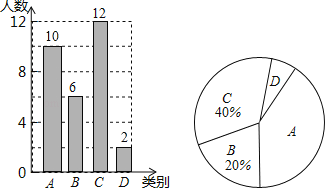
(2)①设D类人数为a,则A类人数为5a,
根据题意,得:a+6+12+5a=30,
解得:a=2,
即A类人数为10、D类人数为2,
补全图形如下:
②扇形图中,“A”对应扇形的圆心角为360°×![]() =120°,
=120°,
故答案为:120;
③估计大约6月1日这天行走的步数超过10000步的好友人数为150×![]() =70人.
=70人.


科目:初中数学 来源: 题型:
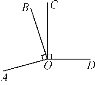
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD交于点O,OM⊥AB,
(1)若∠1=∠2,试判断ON与CD的位置关系,并说明理由.
(2)若∠1=![]() ∠BOC,试求∠MOD的度数.
∠BOC,试求∠MOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.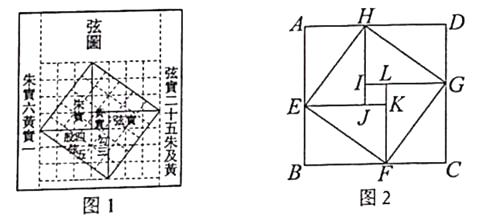
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为( )

A. 3 B. 4 C. 3.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.

(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D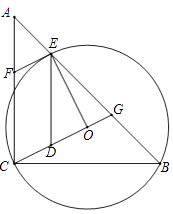
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知∠AOB=∠COD=90°,试写出两个与图①中角(直角除外)有关的结论:
(ⅰ)∠__ __=∠__ __,
(ⅱ)∠__ __+∠__ __=180°;
(2)请选择(1)中的一个结论说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com