
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,3),B(5,1),C(1,3),结合所给的平面直角坐标系,解答下列问题:
(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于x轴对称的△A′B′C′,并写出△A′B′C′各顶点坐标;
(3)在x轴上找一点P,使PA+PB的值最小。请画出点P,并求出点P坐标。
【答案】(1)见解析;(2)图见解析,A′(2,3),B′(5,1),C′(1,3);(3)P(![]() ,0).
,0).
【解析】
(1)在坐标系内描出各点,顺次连接各点即可;
(2)分别作出各点关于x轴的对称点,再顺次连接,并写出各点坐标即可;
(3)连接AB′交x轴于点P,则点P即为所求,利用待定系数法求出直线AB′的解析式,进而可得出P点坐标.
(1)如图,△ABC即为所求;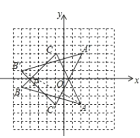
(2)根据轴对称的性质得到 A′(2,3),B′(5,1),C′(1,3),将A′(2,3),B′(5,1),C′(1,3)标在图中,依次连接,如图,△A′B′C′即为所求;
(3)连接AB′交x轴于点P,则点P即为所求。
设直线AB′的解析式为y=kx+b(k≠0),
∵A(2,3),B′(5,1),
∴![]() ,解得
,解得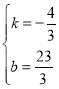 ,
,
∴直线AB′的解析式为y=![]() x+
x+![]() ,
,
∴P(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】美丽的洪泽湖周边景点密布.如图A,B为湖滨的两个景点,C为湖心一个景点.景点B在景点C的正东,从景点A看,景点B在北偏东75°方向,景点C在北偏东30°方向.一游客自景点![]() 驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?
驾船以每分钟20米的速度行驶了10分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间(精确到1分钟)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.
的中点.
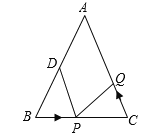
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等, ![]() 与
与![]() 是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
是否可能全等?若能,求出全等时点Q的运动速度和时间;若不能,请说明理由.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿![]() 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在![]() 的哪条边上相遇?
的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() .点
.点![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),连接
重合),连接![]() ,以
,以![]() 为边在
为边在![]() 的右侧作
的右侧作![]() ,且
,且![]() ,
,![]() .
.
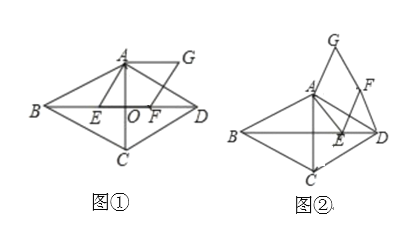
(1)如图①,若点![]() 落在线段
落在线段![]() 上,则线段
上,则线段![]() 与线段
与线段![]() 的数量关系是______;
的数量关系是______;
(2)如图②,若点![]() 不在线段
不在线段![]() 上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
上,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正整数a,我们规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=![]() .例如f(15)=3×15+1=46,f(8)=
.例如f(15)=3×15+1=46,f(8)=![]() =4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
=4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
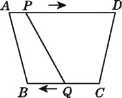
【题目】如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则________后四边形ABQP为平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com