
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
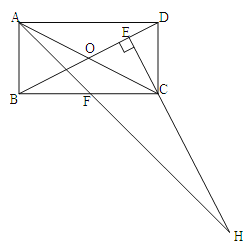
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
(A)1个 (B)2个 (C)3个 (D)4个
【答案】C
【解析】
试题根据矩形的性质可得OA=OB=OC=OD,由AD=![]() ,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
,AB=1根据特殊角的锐角三角函数值可求出∠ADB=30°,即得∠ABO=60°,从而可证得△ABO是等边三角形,即得AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,再依次分析各小题即可作出判断.
根据已知条件不能推出AF=FH,故①错误;
解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AD=![]() ,AB=1,
,AB=1,
∴tan∠ADB=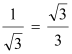 ,
,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,故②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,故③正确;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,
∵CE⊥BD,
∴DE=EO=![]() DO=
DO=![]() BD,
BD,
∴BE=3ED,故④正确;
∴正确的有3个,
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正整数a,我们规定:若a为奇数,则f(a)=3a+1;若a为偶数,则f(a)=![]() .例如f(15)=3×15+1=46,f(8)=
.例如f(15)=3×15+1=46,f(8)=![]() =4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
=4,若a1=16,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a1+a2+a3+…+a2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
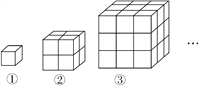
【题目】如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中共有1个小立方体,其中1个看得见,0个看不见;如图②中共有8个小立方体,其中7个看得见,1个看不见;如图③中共有27个小立方体,其中19个看得见,8个看不见,…
(1)第6个图形中,看得见的小立方体有___个;
(2)猜想并写出第n个图形中看不见的小立方体的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司员工住在![]() 三个住宅区,已知
三个住宅区,已知![]() 区有2人,
区有2人,![]() 区有7人,
区有7人,![]() 区有12人,三个住宅区在同一条直线上,且
区有12人,三个住宅区在同一条直线上,且![]() ,
,![]() 是
是![]() 的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在
的中点.为方便员工,公司计划开设通勤车免费接送员工上下班,但因为停车紧张,在![]() 四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
四处只能设一个通勤车停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠站应设在( )
![]()
A.![]() 处B.
处B.![]() 处C.
处C.![]() 处D.
处D.![]() 处
处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
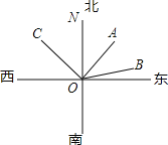
(1)求∠BOC的度数;
(2)求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
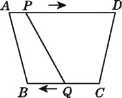
【题目】如图,在四边形ABCD中,AD∥BC,且AD>BC,BC=6 cm,动点P,Q分别从A,C同时出发,P以1 cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则________后四边形ABQP为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
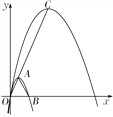
【题目】如图,抛物线C1:y=-![]() x2+2
x2+2![]() x的顶点为A,与x轴的正半轴交于点B.
x的顶点为A,与x轴的正半轴交于点B.
(1)将抛物线C1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的表达式;
(2)将抛物线C1上的点(x,y)变为(kx,ky)(|k|>1),变换后得到的抛物线记作C2,抛物线C2的顶点为C,求抛物线C2的表达式(用k表示);
(3)在(2)条件下,点P在抛物线C2上,满足S△PAC=S△ABC,且∠ACP=90°.当k>1时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com