
【题目】如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中共有1个小立方体,其中1个看得见,0个看不见;如图②中共有8个小立方体,其中7个看得见,1个看不见;如图③中共有27个小立方体,其中19个看得见,8个看不见,…
(1)第6个图形中,看得见的小立方体有___个;
(2)猜想并写出第n个图形中看不见的小立方体的个数.
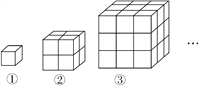
【答案】(1)91;(2)(n-1)3个.
【解析】由题意可知,共有小立方体个数为序号数×序号数×序号数,看不见的小正方体的个数=(序号数-1)×(序号数-1)×(序号数-1),看得见的小立方体的个数为共有小立方体个数减去看不见的小正方体的个数.
(1)当n=1时,看不见的小立方体的个数为(1-1)3=0(个);
当n=2时,看不见的小立方体的个数为(2-1)3=1(个);
当n=3时,看不见的小立方体的个数为(3-1)3=8(个);
…
当n=6时,看不见的小立方体的个数为(6-1)3=125(个),
∴看得见的小立方体有63-125=216-125=91(个);
(2)第n个图形中看不见的小立方体的个数为(n-1)3个.


科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
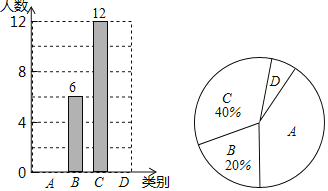
请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 在直线
在直线![]() 上,点
上,点![]() 都在直线
都在直线![]() 上(点
上(点![]() 在点
在点![]() 的左侧),连接
的左侧),连接![]() ,
,![]() 平分
平分![]() 且
且![]()

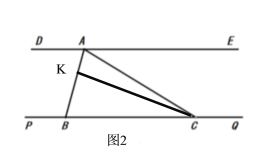
(1)如图1,求证: ![]()
(2)如图2,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)在(2)的条件下,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
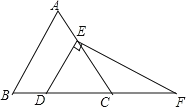
【题目】在等边三角形ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
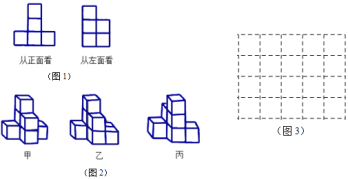
【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
![]() 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______;
![]() 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
![]() 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE![]() BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
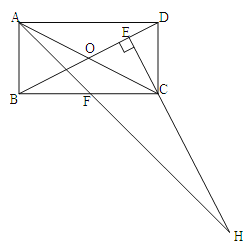
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com