
【题目】已知:点![]() 在直线
在直线![]() 上,点
上,点![]() 都在直线
都在直线![]() 上(点
上(点![]() 在点
在点![]() 的左侧),连接
的左侧),连接![]() ,
,![]() 平分
平分![]() 且
且![]()

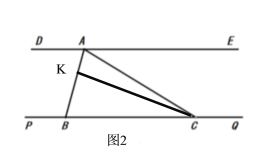
(1)如图1,求证: ![]()
(2)如图2,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数
的度数
(3)在(2)的条件下,点![]() 在直线
在直线![]() 上,连接
上,连接![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的度数(要求:在备用图中画出图形后,再计算)
的度数(要求:在备用图中画出图形后,再计算)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
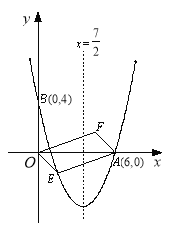
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
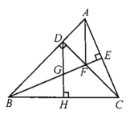
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 于点D,BE平分
于点D,BE平分![]() ,且
,且![]() 于点E与CD相交于点F,
于点E与CD相交于点F,![]() 于点H,交BE于点G,下列结论:①
于点H,交BE于点G,下列结论:①![]() ;②
;②![]() ;③
;③![]() ④
④![]() ;其中正确的是___________.
;其中正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
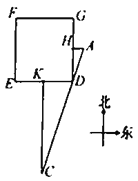
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
查看答案和解析>>
科目:初中数学 来源: 题型:
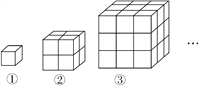
【题目】如图,观察由棱长为1的小立方体摆成的图形,寻找规律:如图①中共有1个小立方体,其中1个看得见,0个看不见;如图②中共有8个小立方体,其中7个看得见,1个看不见;如图③中共有27个小立方体,其中19个看得见,8个看不见,…
(1)第6个图形中,看得见的小立方体有___个;
(2)猜想并写出第n个图形中看不见的小立方体的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
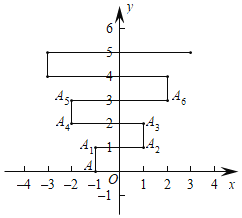
【题目】如图,在平面直角坐标系上有个点A(﹣1,0),点A第1次向上跳动1个单位至点A1(﹣1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位至点A3,第4次向左跳动3个单位至点A4,第5次又向上跳动1个单位至点A5,第6次向右跳动4个单位至点A6,……,依此规律跳动下去,点A第2019次跳动至点A2019的坐标是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com