【题目】某商场购进了一批
、
两种型号的智能扫地机器人，这两种智能扫地机器人的进购数量、进价、售价如表所示：
类型 | 进购数量（个） | 进价（元/个） | 售价（元/个） |
| 20 | 1800 | 2300 |
| 40 | 1500 | ？ |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元，则型智能扫地机器人的销售单价至少是多少元？
快乐5加2金卷系列答案科目：初中数学 来源： 题型：
【题目】（阅读材料）
我们知道“在数轴上表示的两个数，右边的数总比左边的数大”，利用此规律，我们可以求数轴上两个点之间的距离，具体方法是：用右边的数减去左边的数的差就是表示这两个数的两点之间的距离．若点
表示的数是
，点
表示的数是
，点在点的右边（即
），则点，之间的距离为
（即
）．
例如：若点
表示的数是－6，点
表示的数是－9，则线段
．
（理解应用）
（1）已知在数轴上，点
表示的数是－2020，点
表示的数是2020，求线段
的长；
（拓展应用）
如图，数轴上有三个点，点
表示的数是－2，点
表示的数是3，点
表示的数是
．
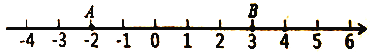
（2）当，，三个点中，其中一个点是另外两个点所连线段的中点时，求的值；
（3）在点左侧是否存在一点
，使点到点，点的距离和为19？若存在，求出点表示的数：若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知正方形ABCD的边长为6，E、F、P分别是AB、CD、AD上的点（均不与正方形顶点重合）且PE=PF,PE⊥PF.
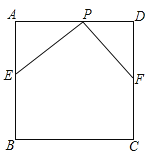
（1）求证：AE+DF=6
（2）设AE=
，五边形EBCFP的面积为
，求与的函数关系式，并求出的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：
中，
，求证：
.下面给出运用反证法证明的四个步骤：①∴
，这与三角形内角和为
矛盾
②因此假设不成立.∴
③假设在中，
④由，得
，即
这四个步骤正确的顺序应是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一辆汽车行驶时的耗油量为0.1升/千米，如图是油箱剩余油量
（升）关于加满油后已行驶的路程
（千米）的函数图象.
（1）根据图象，直接写出汽车行驶400千米时，油箱内的剩余油量，并计算加满油时油箱的油量；
（2）求关于的函数关系式，并计算该汽车在剩余油量5升时，已行驶的路程.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点
在直线
上，点
都在直线
上（点
在点
的左侧），连接
，
平分
且
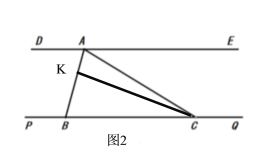
（1）如图1，求证： 
（2）如图2，点
为上一点，连接
，若
，求
的度数
（3）在（2）的条件下，点
在直线上，连接
，且
，若
，求
的度数（要求：在备用图中画出图形后，再计算）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列代数式或方程解应用题：
已知小明的年龄是
岁，小红的年龄比小明的年龄的
倍小
岁，小华的年龄比小红的年龄大
岁，求这三名同学的年龄的和．
小亮与小明从学校同时出发去看在首都体育馆举行的一场足球赛， 小亮每分钟走
，他走到足球场等了
分钟比赛才开始：小明每分钟走
，他走到足球场，比赛已经开始了
分钟．问学校与足球场之间的距离有多远?
请根据图中提供的信息，回答下列问题：
①一个水瓶与一个水杯分别是多少元?
②甲、乙两家商场都销售该水瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打八折；乙商场规定：买一个水瓶赠送两个水杯，单独购买的水杯仍按原价销售．若某单位想在一家商场买个水瓶和
个水杯，请问选择哪家商场更合算?请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
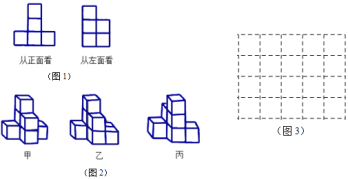
【题目】一个由若干小正方形堆成的几何体，它从正面看和从左面看的图形如图1所示．
这个几何体可以是图2中甲，乙，丙中的______；
这个几何体最多由______个小正方体堆成，最少由______个小正方体堆成；
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
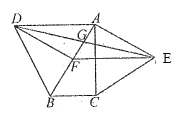
【题目】如图，分别以
的斜边
，直角边
为边向外作等边
和
，
为的中点，
，相交于点
.若∠BAC=30°，下列结论：①
；②四边形
为平行四边形；③
；④
.其中正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
