
【题目】已知正方形ABCD的边长为6,E、F、P分别是AB、CD、AD上的点(均不与正方形顶点重合)且PE=PF,PE⊥PF.
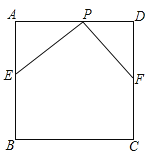
(1)求证:AE+DF=6
(2)设AE=![]() ,五边形EBCFP的面积为
,五边形EBCFP的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;
(2)y=x26x+36,y的取值范围是27≤y<36.
【解析】
(1)根据∠A=∠D=∠EPF=90°和PE=PF的条件,易证△AEP与△DPF全等,根据全等三角形的对应边相等即可得证;
(2)可以用x表示PD进而表示AP,五边形面积y等于正方形面积减去两个全等三角形的面积,写得y的函数解析式.把函数解析式写出顶点式,结合x的取值范围求出y的取值范围.,
(1)∵四边形ABCD是正方形,
∴AB=BC=CD=DA=6,∠A=∠D=90°,
∴∠AEP+∠APE=90°,
∵PE⊥PF,
∴∠EPF=90°,
∴∠APE+∠DPF=90°,
∴∠AEP=∠DPF,
在△AEP与△DPF中,
 ,
,
∴△AEP≌△DPF(AAS),
∴AE=DP AP=DF,
∴DP+AP=AD=6;
(2)∵△AEP≌△DPF,
∴S△AEP=S△DPF,DP=AE=x,
∴AP=ADDP=6x,
∴y=S正方形ABCDS△AEP=S△DPF=S正方形ABCD2S△AEP=AB22![]() AEAP=36x(6x)=x26x+36=(x3)2+27,
AEAP=36x(6x)=x26x+36=(x3)2+27,
∵0<x<6,
∴x=3时,y最小值为27;x=0或6时,y=(03)2+27=36,
∴27≤y<36,
∴y=x26x+36,y的取值范围是27≤y<36.


科目:初中数学 来源: 题型:
【题目】某同学准备报名参加运动会,有以下4个项目可供选择. 径赛项目:100m,200m (分别用A 、B表示);田赛项目:跳远 ,跳高(分别用C 、D表示).
(1)该同学从4个项目中任选一个,恰好是田赛项目的概率为 ;
(2)该同学从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果(请用A、B、C、D表示相对应的项目),并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则A2017的坐标为( )
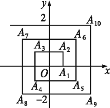
A.(505,504)B.(505,-504)C.(-504,504)D.(-504,-504)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
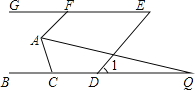
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
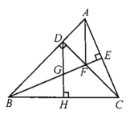
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 于点D,BE平分
于点D,BE平分![]() ,且
,且![]() 于点E与CD相交于点F,
于点E与CD相交于点F,![]() 于点H,交BE于点G,下列结论:①
于点H,交BE于点G,下列结论:①![]() ;②
;②![]() ;③
;③![]() ④
④![]() ;其中正确的是___________.
;其中正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了一批![]() 、
、![]() 两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
两种型号的智能扫地机器人,这两种智能扫地机器人的进购数量、进价、售价如表所示:
类型 | 进购数量(个) | 进价(元/个) | 售价(元/个) |
| 20 | 1800 | 2300 |
| 40 | 1500 | ? |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元,则![]() 型智能扫地机器人的销售单价至少是多少元?
型智能扫地机器人的销售单价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?
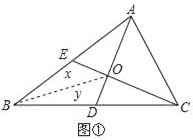
(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
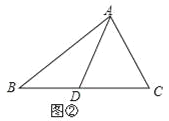
小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有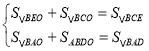 即
即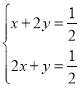 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
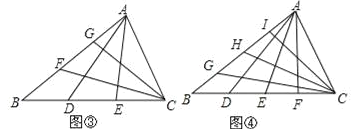
②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com