
����Ŀ������һ���ڼ䣬С����С�¼����ڵ�����������棬�ڴ�ͷA��С���ӵ�С�·����Ķ�λ������С�¼�C���Լ��ı�ƫ��45�����������غӱ߱�ֱ���̵�l����200����B������ʱ��λ��ʾС�¼�C���Լ��ı�ƫ��30��������ͼ��ʾ������������Ϣ������ĶԻ��������С����һ�����������̵�����ֱ�߶����ײ��ܵ�����ͷD������ȷ��1�ף����������ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
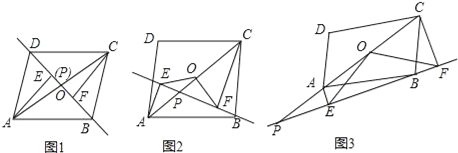
����Ŀ����֪����P��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��P�����A��C�غϣ����ֱ����A��C��ֱ��BP�����ߣ�����ֱ�Ϊ��E��F����OΪAC���е㣮��1������P���O�غ�ʱ��ͼ1����֤OE=OF������֤����
��2��ֱ��BP�Ƶ�B��ʱ�뷽����ת������OFE=30��ʱ����ͼ2��ͼ3��λ�ã������߶�CF��AE��OE֮����������������ϵ����д�����ͼ2��ͼ3�IJ��룬��ѡ��һ���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
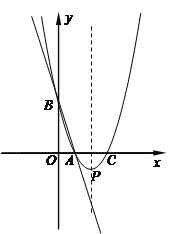
����Ŀ����ͼ��ֱ��y����3x��3��x�ᡢy��ֱ��ڵ�A��B��������y=a��x��2��2��k������A��B������x�ύ����һ��C���䶥��ΪP��
��1����a��k��ֵ��
��2�������ߵĶԳ������Ƿ����һ��M��ʹ��ABM���ܳ���С�������ڣ������ABM���ܳ����������ڣ���˵�����ɣ�
��3������ABΪֱ����Բ���������ߵĶԳ��ύ�ڵ�N�������N���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ķ����ϣ�
����֪�����������ϱ�ʾ�����������ұߵ����ܱ���ߵ������������ô˹��ɣ����ǿ�����������������֮��ľ��룬���巽���ǣ����ұߵ�����ȥ��ߵ����IJ���DZ�ʾ��������������֮��ľ��룮����![]() ��ʾ������
��ʾ������![]() ����
����![]() ��ʾ������
��ʾ������![]() ����
����![]() �ڵ�
�ڵ�![]() ���ұߣ���
���ұߣ���![]() �������
�������![]() ��
��![]() ֮��ľ���Ϊ
֮��ľ���Ϊ![]() ����
����![]() ����
����
���磺����![]() ��ʾ�����ǣ�6����
��ʾ�����ǣ�6����![]() ��ʾ�����ǣ�9�����߶�
��ʾ�����ǣ�9�����߶�![]() ��
��
������Ӧ�ã�
��1����֪�������ϣ���![]() ��ʾ�����ǣ�2020����
��ʾ�����ǣ�2020����![]() ��ʾ������2020�����߶�
��ʾ������2020�����߶�![]() �ij���
�ij���
����չӦ�ã�
��ͼ���������������㣬��![]() ��ʾ�����ǣ�2����
��ʾ�����ǣ�2����![]() ��ʾ������3����
��ʾ������3����![]() ��ʾ������
��ʾ������![]() ��
��
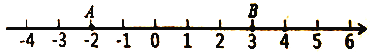
��2����![]() ��
��![]() ��
��![]() �������У�����һ���������������������߶ε��е�ʱ����
�������У�����һ���������������������߶ε��е�ʱ����![]() ��ֵ��
��ֵ��
��3���ڵ�![]() ����Ƿ����һ��
����Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ����
����![]() ����
����![]() �ľ����Ϊ19�������ڣ������
�ľ����Ϊ19�������ڣ������![]() ��ʾ�������������ڣ���˵�����ɣ�
��ʾ�������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬
��һ�㣬![]() ƽ��
ƽ��![]() �������½�����ȷ����______����ֻ����ţ���
�������½�����ȷ����______����ֻ����ţ���![]() ��
��![]() ��Ϊ��ǣ�����
��Ϊ��ǣ�����![]() ����
����![]() ����
����![]() ;��
;��![]() ƽ��
ƽ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֱ�����ǰ�![]() ��ֱ�Ƕ���
��ֱ�Ƕ���![]() ��ֱ��
��ֱ��![]() �ϣ�������
�ϣ�������![]() ���ǰ�ĸ��ߺ�����
���ǰ�ĸ��ߺ�����![]() ������ֱ��
������ֱ��![]() ���Ϸ���
���Ϸ���
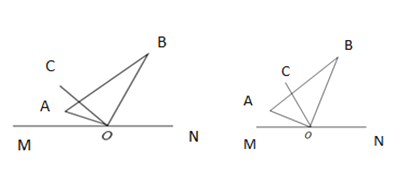
��1�������ǰ���![]() ����ƽ������ת����
����ƽ������ת����![]() ƽ��
ƽ��![]() ʱ����ͼ1�����
ʱ����ͼ1�����![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ2�������ǰ�![]() ��
��![]() ����ƽ��������ת�������
����ƽ��������ת�������![]() ʼ����
ʼ����![]() �ڣ���
�ڣ���![]() �����ʣ�
�����ʣ�![]() ��
��![]() ��������������ϵ?
��������������ϵ?
��3����ͼ2�����![]() ƽ��
ƽ��![]() ��
��![]() �Ƿ�Ҳƽ��
�Ƿ�Ҳƽ��![]() ?��˵�����ɣ�
?��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��ֱ��
��ֱ��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�
��1������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��ͬ�࣬��
��ͬ�࣬��![]() ��
��![]() ���ڲ�ʱ����ͼ1��ʾ ���� ��
���ڲ�ʱ����ͼ1��ʾ ���� ��![]() ����
����![]() �Ĵ�С��
�Ĵ�С��
��2������![]() ���
���![]() ��ֱ��
��ֱ��![]() �����ԣ���ͼ2��ʾ������1���еĽ����Ƿ���Ȼ�������������Ľ��ۣ���˵�����ɣ�
�����ԣ���ͼ2��ʾ������1���еĽ����Ƿ���Ȼ�������������Ľ��ۣ���˵�����ɣ�
��3����ͼ2 �е�����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ���õ�����
���õ�����![]() ����
����![]() ����
����![]() ����
����![]() �Ķ����� ���ú�
�Ķ����� ���ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD�ı߳�Ϊ6��E��F��P�ֱ���AB��CD��AD�ϵĵ㣨�����������ζ����غϣ���PE=PF,PE��PF.
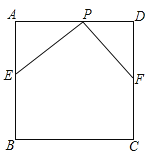
��1����֤��AE+DF=6
��2����AE=![]() �������EBCFP�����Ϊ
�������EBCFP�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���д���ʽ�̽�Ӧ���⣺
![]() ��֪С����������
��֪С����������![]() �꣬С��������С���������
�꣬С��������С���������![]() ��С
��С![]() �꣬С���������С��������
�꣬С���������С��������![]() �꣬��������ͬѧ������ĺͣ�
�꣬��������ͬѧ������ĺͣ�
![]() С����С����ѧУͬʱ����ȥ�����������ݾ��е�һ���������� С��ÿ������
С����С����ѧУͬʱ����ȥ�����������ݾ��е�һ���������� С��ÿ������![]() �����ߵ�������
�����ߵ�������![]() ���ӱ����ſ�ʼ��С��ÿ������
���ӱ����ſ�ʼ��С��ÿ������![]() �����ߵ����������Ѿ���ʼ��
�����ߵ����������Ѿ���ʼ��![]() ���ӣ���ѧУ������֮��ľ����ж�Զ?
���ӣ���ѧУ������֮��ľ����ж�Զ?
![]() �����ͼ���ṩ����Ϣ���ش��������⣺
�����ͼ���ṩ����Ϣ���ش��������⣺

��һ��ˮƿ��һ��ˮ���ֱ��Ƕ���Ԫ?
�ڼס��������̳������۸�ˮƿ��ˮ����Ϊ��ӭ�����꣬�����̳����ڸ����������̳��涨����������Ʒ������ۣ����̳��涨����һ��ˮƿ��������ˮ�������������ˮ����ԭ�����ۣ���ij��λ����һ���̳���![]() ��ˮƿ��
��ˮƿ��![]() ��ˮ��������ѡ���ļ��̳�������?��˵�����ɣ�
��ˮ��������ѡ���ļ��̳�������?��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com