
【题目】一直角三角板![]() 的直角顶点
的直角顶点![]() 在直线
在直线![]() 上,作射线
上,作射线![]() 三角板的各边和射线
三角板的各边和射线![]() 都处于直线
都处于直线![]() 的上方.
的上方.
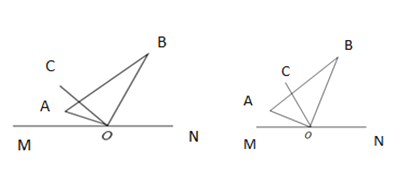
(1)将三角板绕![]() 点在平面内旋转,当
点在平面内旋转,当![]() 平分
平分![]() 时,如图1,如果
时,如图1,如果![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,将三角板![]() 绕
绕![]() 点在平面内任意转动,如果
点在平面内任意转动,如果![]() 始终在
始终在![]() 内,且
内,且![]() ,请问:
,请问:![]() 和
和![]() 有怎样的数量关系?
有怎样的数量关系?
(3)如图2,如果![]() 平分
平分![]() ,
,![]() 是否也平分
是否也平分![]() ?请说明理由.
?请说明理由.
【答案】(1)![]() ;(2)∠BOC-∠AOM=
;(2)∠BOC-∠AOM=![]() ;(3)OB平分∠CON.理由见解析
;(3)OB平分∠CON.理由见解析
【解析】
(1)根据角平分线的意义可得∠COM=∠BOC=65°,再根据互余可求出∠AOC的度数;
(2)当OA始终在∠COM的内部时,有∠AOM+∠AOC=65°,∠AOC+∠BOC=90°,进而得出∠AOM与∠BOC的等量关系;
(3)根据余角的性质得出∠AOM+∠BOC=90°,再证明∠AOM+∠BON=90°,即可得出结论.
解:(1)∵![]() 平分
平分![]() ,
,
∴∠COM=∠BOC=65°,
又∵∠AOC+∠BOC=90°,
∴∠AOC=90°-65°=25°;
(2)∵OA始终在∠COM的内部,
∠COM=∠AOM+∠AOC=65°,
∴∠AOC=65°-∠AOM,
又∵∠AOC+∠BOC=90°,
∴65°-∠AOM+∠BOC=90°,
∴∠BOC-∠AOM=![]() ;
;
(3)∵![]() 平分
平分![]() ,
,
∴∠AOM=∠AOC,
又∵∠AOC+∠BOC=90°,
∴∠AOM+∠BOC=90°,
∵∠AOB=90°,
∴∠AOM+∠BON=90°,
∴∠BOC=∠BON,
∴![]() 平分
平分![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】在数轴上,点![]() 分别表示数
分别表示数![]() ,且
,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右运动,点
个单位长度的速度沿数轴向右运动,点![]() 始终为线段
始终为线段![]() 的中点,设点
的中点,设点![]() 运动的时间为
运动的时间为![]() 秒.则:
秒.则:
![]()
![]() 在点
在点![]() 运动过程中,用含
运动过程中,用含![]() 的式子表示点
的式子表示点![]() 在数轴上所表示的数.
在数轴上所表示的数.
![]() 当
当![]() 时,点
时,点![]() 在数轴上对应的数是什么?
在数轴上对应的数是什么?
![]() 设点
设点![]() 始终为线段
始终为线段![]() 的中点,某同学发现,当点
的中点,某同学发现,当点![]() 运动到点
运动到点![]() 右侧时,线段
右侧时,线段![]() 长度始终不变.请你判断该同学的说法是否正确,并加以证明.
长度始终不变.请你判断该同学的说法是否正确,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF的长是( )
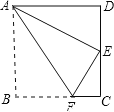
A. 7.5 B. 8 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
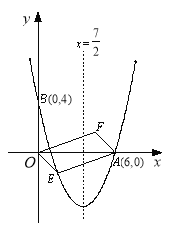
【题目】如图,对称轴为直线x=![]() 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)①当四边形OEAF的面积为24时,请判断OEAF是否为菱形?
②是否存在点E,使四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
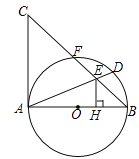
【题目】如图,已知AB为⊙O直径,AC是⊙O的切线,连接BC交⊙O于点F,取![]() 的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
的中点D,连接AD交BC于点E,过点E作EH⊥AB于H.
(1)求证:△HBE∽△ABC;
(2)若CF=4,BF=5,求AC和EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则A2017的坐标为( )
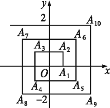
A.(505,504)B.(505,-504)C.(-504,504)D.(-504,-504)
查看答案和解析>>
科目:初中数学 来源: 题型:
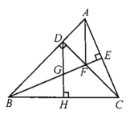
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() 于点D,BE平分
于点D,BE平分![]() ,且
,且![]() 于点E与CD相交于点F,
于点E与CD相交于点F,![]() 于点H,交BE于点G,下列结论:①
于点H,交BE于点G,下列结论:①![]() ;②
;②![]() ;③
;③![]() ④
④![]() ;其中正确的是___________.
;其中正确的是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
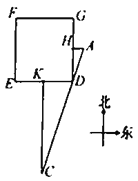
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,![]() 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门
是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门![]() 位于
位于![]() 的中点,南门
的中点,南门![]() 位于
位于![]() 的中点,出东门15步的
的中点,出东门15步的![]() 处有一树木,求出南门多少步恰好看到位于
处有一树木,求出南门多少步恰好看到位于![]() 处的树木(即点
处的树木(即点![]() 在直线
在直线![]() 上)?请你计算
上)?请你计算![]() 的长为__________步.
的长为__________步.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com