练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

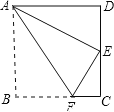
    【题目】如图，四边形ABCD为矩形纸片．把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF．若CD=6，则AF的长是( )

    A. 7.5 B. 8 C. D.

    【答案】D

    【解析】先图形折叠的性质得到BF=EF，AE=AB，再由E是CD的中点可求出ED的长，再求出∠EAD的度数，设FE=x，则AF=2x，在△ADE中利用勾股定理即可求解．

    由折叠的性质得BF=EF，AE=AB，
    因为CD=6，E为CD中点，故ED=3，
    又因为AE=AB=CD=6，
    所以∠EAD=30°，
    则∠FAE=（90°-30°）=30°，
    设FE=x，则AF=2x，
    在△AEF中，根据勾股定理，（2x）2=62+x2，
    x2=12，x1=2，x2=-2（舍去）．
    AF=2×2=4．

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】 某公园准备修建一块长方形草坪，长为a米，宽为b米．并在草坪上修建如图所示的十字路,

    已知十字路宽2米.

    （1）用含a、b的代数式表示修建的十字路的面积.

    （2）若a=30，b=20，求草坪（阴影部分）的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，∠E＝∠F＝90°，∠B＝∠C，AE＝AF，结论：①EM＝FN；②AF

    ∥EB；③∠FAN＝∠EAM；④△ACN≌△ABM其中正确的有 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（ ）

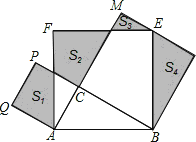
    A．14 B．16 C．18 D．20

    查看答案和解析>>

    科目：初中数学 来源： 题型：

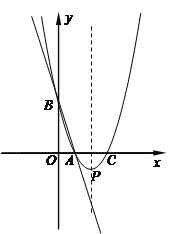
    【题目】如图，直线y＝－3x＋3与x轴、y轴分别交于点A、B，抛物线y=a（x－2）2＋k经过点A、B，并与x轴交于另一点C，其顶点为P．

    （1）求a，k的值；

    （2）抛物线的对称轴上是否存在一点M，使△ABM的周长最小，若存在，求出△ABM的周长；若不存在，请说明理由；

    （3）若以AB为直径画圆，与抛物线的对称轴交于点N，求出点N坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】灌云教育局为了解今年九年级学生体育测试情况，随机抽查了部分学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：

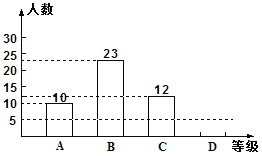
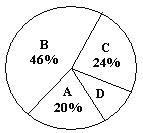
    （说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）

    （1）请把条形统计图补充完整；

    （2）样本中D级的学生人数占全班学生人数的百分比是_____________；

    （3）扇形统计图中A级所在的扇形的圆心角度数是_____________；

    （4）若该县九年级有8000名学生，请你用此样本估计体育测试中A级和B级的学生人数之和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读材料）

    我们知道“在数轴上表示的两个数，右边的数总比左边的数大”，利用此规律，我们可以求数轴上两个点之间的距离，具体方法是：用右边的数减去左边的数的差就是表示这两个数的两点之间的距离．若点表示的数是，点表示的数是，点在点的右边（即），则点，之间的距离为（即）．

    例如：若点表示的数是－6，点表示的数是－9，则线段．

    （理解应用）

    （1）已知在数轴上，点表示的数是－2020，点表示的数是2020，求线段的长；

    （拓展应用）

    如图，数轴上有三个点，点表示的数是－2，点表示的数是3，点表示的数是．

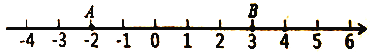
    （2）当，，三个点中，其中一个点是另外两个点所连线段的中点时，求的值；

    （3）在点左侧是否存在一点，使点到点，点的距离和为19？若存在，求出点表示的数：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一直角三角板的直角顶点在直线上，作射线三角板的各边和射线都处于直线的上方．

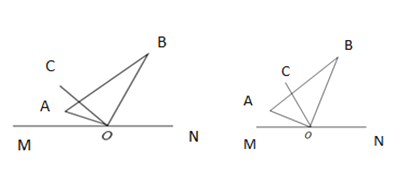
    （1）将三角板绕点在平面内旋转，当平分时，如图1，如果，求的度数；

    （2）如图2，将三角板绕点在平面内任意转动，如果始终在内，且，请问： 和有怎样的数量关系?

    （3）如图2，如果平分，是否也平分?请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：中，，求证：.下面给出运用反证法证明的四个步骤：①∴，这与三角形内角和为矛盾

    ②因此假设不成立.∴

    ③假设在中，

    ④由，得，即

    这四个步骤正确的顺序应是______.

    查看答案和解析>>

    同步练习册答案