
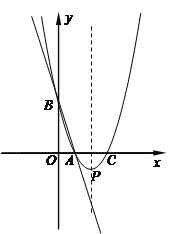
【题目】如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
(1)求a,k的值;
(2)抛物线的对称轴上是否存在一点M,使△ABM的周长最小,若存在,求出△ABM的周长;若不存在,请说明理由;
(3)若以AB为直径画圆,与抛物线的对称轴交于点N,求出点N坐标.
【答案】(1)a,k的值分别为1,﹣1;(2)![]() ,理由见解析;(3)点N的坐标为(2,2)或(2,1)
,理由见解析;(3)点N的坐标为(2,2)或(2,1)
【解析】(1)由条件可先求得A、B坐标,代入抛物线解析式可求得a、k的值;
(2)由A、C关于对称轴对称,连接BC交对称轴于点M,则M即为所求,由B、C可求得直线BC的解析式,可求得M点的坐标,容易求得其周长;
(3)可设N点坐标为(2,n),可分别表示出AB、AN、BN的长,由勾股定理可得到关于n的方程,可求得N点坐标.
(1)∵直线y=﹣3x+3与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,3).
又∵抛物线抛物线y=a(x﹣2)2+k经过点A(1,0),B(0,3),
∴![]()
解得![]()
故a,k的值分别为1,﹣1;
(2)如图1,存在这样的点M.连接BC与对称轴x=2的交点即为M点,这时△ABM的周长最小.
由抛物线对称性可得,点C坐标为(3,0),
△ABM的周长=AB+AM+BM
=AB+BC
=![]() ;
;
(3)如图2,由题意,可设N点的坐标为(2,n),对称轴x=2交x轴于点F,过点B作BE垂直于直线x=2于点E.
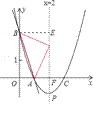
∵AB为所作圆的直径,N为所作圆与直线x=2的交点,
∴∠ANB=90°.
在Rt△ANF中,AN2=AF2+NF2=1+n2,
在Rt△BNE中,BN2=BE2+EN2=4+(3﹣n)2,
由勾股定理,得到方程1+n2+4+(3﹣n)2=12+32,
化简,得n2﹣3n +2=0,
解得 n1=2,n2=1,
∴点N的坐标为(2,2)或(2,1).


科目:初中数学 来源: 题型:
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
查看答案和解析>>
科目:初中数学 来源: 题型:
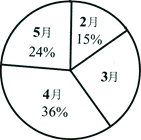
【题目】2010年4月,国务院出台“房贷新政”,确定实行更为严格的差别化住房信贷政策,对楼市产生了较大的影响.下面是某市今年2月~5月商品住宅的月成交量统计图(不完整),请根据图中提供的信息,完成下列问题:
(1)该市今年2月~5月共成交商品住宅______套;
(2)请你补全条形统计图;
(3)该市这4个月商品住宅的月成交量的极差是____套,中位数是_______套.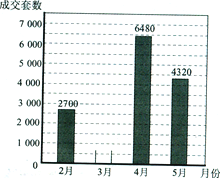
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学准备报名参加运动会,有以下4个项目可供选择. 径赛项目:100m,200m (分别用A 、B表示);田赛项目:跳远 ,跳高(分别用C 、D表示).
(1)该同学从4个项目中任选一个,恰好是田赛项目的概率为 ;
(2)该同学从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果(请用A、B、C、D表示相对应的项目),并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
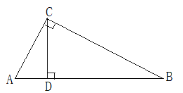
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
(1)求△ABC的面积;
(2)求CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC上的高DF,当BD=![]() 时,试求出DF的长(用
时,试求出DF的长(用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF的长是( )
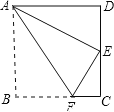
A. 7.5 B. 8 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
(2)已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3950元.则甲、乙车每天的租金分别为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小明到小陈家所在的美丽乡村游玩,在村头A处小明接到小陈发来的定位,发现小陈家C在自己的北偏东45°方向,于是沿河边笔直的绿道l步行200米到达B处,这时定位显示小陈家C在自己的北偏东30°方向,如图所示,根据以上信息和下面的对话,请你帮小明算一算他还需沿绿道继续直走多少米才能到达桥头D处(精确到1米)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com