练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某建筑工地计划租用甲、乙两辆车清理建筑垃圾，已知甲车单独运完需要15天，乙车单独运完需要30天．甲车先运了3天，然后甲、乙两车合作运完剩下的垃圾．

    （1）甲、乙两车合作还需要多少天运完垃圾？

    （2）已知甲车每天的租金比乙车多100元，运完垃圾后建筑工地共需支付租金3950元．则甲、乙车每天的租金分别为多少元？

    【答案】（1）甲、乙两车合作还需要8天运完垃圾；（2）甲车每天租金为250元，乙车每天租金为150元．

    【解析】

    （1）根据题意首先可以得知甲车效率为每天运送，乙车效率为每天运送，据此设甲、乙两车合作还需要天运完垃圾，然后进一步列出方程求解即可；

    （2）设乙车每天租金为元，则甲车每天租金为元，据此根据“共需支付租金3950元”列出方程求解即可.

    （1）设甲、乙两车合作还需要天运完垃圾，

    根据题意，得

    解得：，

    答：甲、乙两车合作还需要8天运完垃圾．

    （2）设乙车每天租金为元，则甲车每天租金为元，

    根据题意，得

    解得：

    （元），

    答：甲车每天租金为250元，乙车每天租金为150元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】按要求画图：（1）如图1平面上有五个点，按下列要求画出图形.

    ①连接；

    ②画直线交于点；

    ③画出线段的反向延长线；

    ④请在直线上确定一点，使两点到点的距离之和最小，并写出画图的依据.

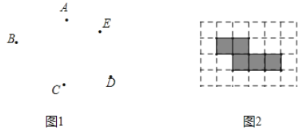
    （2）有5个大小一样的正方形制成如图2所示的拼接图形（阴影部分），请你在图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.（注意：只需添加一个符合要求的正方形，并用阴影表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地图书馆为了满足群众多样化阅读的需求，决定购买甲、乙两种品牌的电脑若干组建电子阅览室．经了解，甲、乙两种品牌的电脑单价分别3100元和4600元．

    （1）若购买甲、乙两种品牌的电脑共50台，恰好支出200000元，求甲、乙两种品牌的电脑各购买了多少台？

    （2）若购买甲、乙两种品牌的电脑共50台，每种品牌至少购买一台，且支出不超过160000元，共有几种购买方案？并说明哪种方案最省钱．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

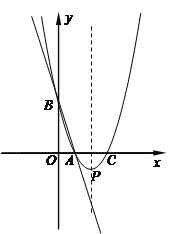
    【题目】如图，直线y＝－3x＋3与x轴、y轴分别交于点A、B，抛物线y=a（x－2）2＋k经过点A、B，并与x轴交于另一点C，其顶点为P．

    （1）求a，k的值；

    （2）抛物线的对称轴上是否存在一点M，使△ABM的周长最小，若存在，求出△ABM的周长；若不存在，请说明理由；

    （3）若以AB为直径画圆，与抛物线的对称轴交于点N，求出点N坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）（观察思考）：

    如图，线段上有两个点,图中共有_________条线段；

    （2）（模型构建）：

    如果线段上有个点（包括线段的两个端点），则该线段上共有___________条线段；

    （3）（拓展应用）：

    某班8位同学参加班上组织的象棋比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），那么一共要进行__________场比赛．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（阅读材料）

    我们知道“在数轴上表示的两个数，右边的数总比左边的数大”，利用此规律，我们可以求数轴上两个点之间的距离，具体方法是：用右边的数减去左边的数的差就是表示这两个数的两点之间的距离．若点表示的数是，点表示的数是，点在点的右边（即），则点，之间的距离为（即）．

    例如：若点表示的数是－6，点表示的数是－9，则线段．

    （理解应用）

    （1）已知在数轴上，点表示的数是－2020，点表示的数是2020，求线段的长；

    （拓展应用）

    如图，数轴上有三个点，点表示的数是－2，点表示的数是3，点表示的数是．

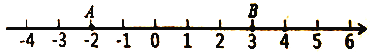
    （2）当，，三个点中，其中一个点是另外两个点所连线段的中点时，求的值；

    （3）在点左侧是否存在一点，使点到点，点的距离和为19？若存在，求出点表示的数：若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为直线上一点，平分，则以下结论正确的有______．（只填序号）①与互为余角；②若，则；③;④平分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点是直线上一点，，是的平分线．

    （1）当点，在直线的同侧，且在的内部时（如图1所示 ）， 设，求的大小；

    （2）当点与点在直线的两旁（如图2所示），（1）中的结论是否仍然成立？请给出你的结论，并说明理由；

    （3）将图2 中的射线绕点顺时针旋转，得到射线，设，若，则的度数是 （用含的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆汽车行驶时的耗油量为0.1升/千米，如图是油箱剩余油量（升）关于加满油后已行驶的路程（千米）的函数图象.

    （1）根据图象，直接写出汽车行驶400千米时，油箱内的剩余油量，并计算加满油时油箱的油量；

    （2）求关于的函数关系式，并计算该汽车在剩余油量5升时，已行驶的路程.

    查看答案和解析>>

    同步练习册答案