
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
【答案】(1)相等;(2)![]() 平方米.
平方米.
【解析】
试题(1)过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,得出△ABC与△AEG的两条高,由正方形的特殊性证明△ACM≌△AGN,是判断△ABC与△AEG面积之间的关系的关键;
(2)同(1)道理知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和,求出这条小路一共占地多少平方米.
试题解析:(1)△ABC与△AEG面积相等.
理由:过点C作CM⊥AB于M,过点G作GN⊥EA交EA延长线于N,则∠AMC=∠ANG=90°,
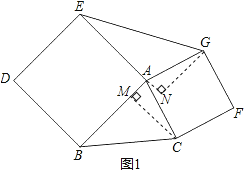
∵四边形ABDE和四边形ACFG都是正方形,
∴∠BAE=∠CAG=90°,AB=AE,AC=AG,
∵∠BAE+∠CAG+∠BAC+∠EAG=360°,
∴∠BAC+∠EAG=180°,
∵∠EAG+∠GAN=180°,
∴∠BAC=∠GAN,
∴△ACM≌△AGN,
∴CM=GN,
∵S△ABC=![]() ABCM,S△AEG=
ABCM,S△AEG=![]() AEGN,
AEGN,
∴S△ABC=S△AEG;
(2)由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和.
∴这条小路的面积为(a+2b)平方米.


科目:初中数学 来源: 题型:
【题目】我们来定义一种新运算:对于任意实数x、y,“※”为a※b=(a+1)(b+1)﹣1
(1)计算(﹣3)※9
(2)嘉琪研究运算“※”之后认为它满足交换律,你认为她的判断 (正确、错误)
(3)请你帮助嘉琪完成她对运算“※”是否满足结合律的证明.
证明:由已知把原式化简得a※b=(a+1)(b+1)﹣1=ab+a+b
∵(a※b)※c=(ab+a+b)※c=
a※(b※c)=
∴
∴运算“※”满足结合律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路边安装路灯,灯柱BC高15m,与灯杆AB的夹角ABC为120°.路灯采用锥形灯罩,照射范围DE长为18.9m,从D、E两处测得路灯A的仰角分别为∠ADE=80.5°,∠AED=45°.求灯杆AB的长度.(参考数据:cos80.5°≈0.2,tan80.5°≈6.0)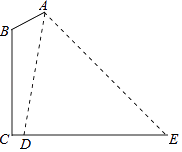
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年是中国人民抗日战争暨世界反法西斯战争胜利70周年,9月3日全国各地将举行有关纪念活动.为了解初中学生对二战历史的知晓情况,某初中课外兴趣小组在本校学生中开展了专题调查活动,随机抽取了部分学生进行问卷调查,根据学生的答题情况,将结果分为A、B、C、D四类,其中A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”;D类表示“不太了解”,调查的数据经整理后形成尚未完成的条形统计图(如图①)和扇形统计图(如图②): 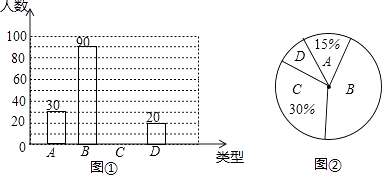
(1)在这次抽样调查中,一共抽查了名学生;
(2)请把图①中的条形统计图补充完整;
(3)图②的扇形统计图中D类部分所对应扇形的圆心角的度数为;
(4)如果这所学校共有初中学生1500名,请你估算该校初中学生中对二战历史“非常了解”和“比较了解”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
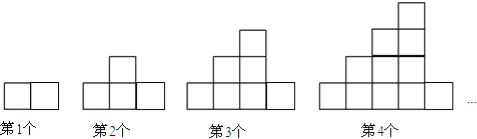
A. 156 B. 157 C. 158 D. 159
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 . 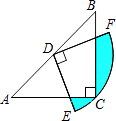
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com