
【题目】已知y是x的反比例函数,且x=8时,y=12.
(1)写出y与x之间的函数关系式;
(2)如果自变量x的取值范围是2≤x≤3,求y的取值范围.
【答案】
(1)
解:设反比例函数的解析式是![]() ,把x=8,y=12代入得:k=96.则函数的解析式是:
,把x=8,y=12代入得:k=96.则函数的解析式是:![]() .
.
(2)
解:在函数![]() 中,令x=2和3,分别求得y的值是:48和32.因而如果自变量x的取值范围是2≤x≤3,y的取值范围是32≤y≤48.
中,令x=2和3,分别求得y的值是:48和32.因而如果自变量x的取值范围是2≤x≤3,y的取值范围是32≤y≤48.
【解析】(1)设反比例函数的解析式是![]() ,把x=8,y=12代入得:k=96.则函数的解析式是:
,把x=8,y=12代入得:k=96.则函数的解析式是:![]() ;(2)在函数
;(2)在函数![]() 中,令x=2和3,分别求得y的值是:48和32.因而如果自变量x的取值范围是2≤x≤3,y的取值范围是32≤y≤48.
中,令x=2和3,分别求得y的值是:48和32.因而如果自变量x的取值范围是2≤x≤3,y的取值范围是32≤y≤48.
【考点精析】根据题目的已知条件,利用反比例函数的概念的相关知识可以得到问题的答案,需要掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数.


科目:初中数学 来源: 题型:
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)求证:BF⊥AF;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明. 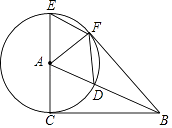
查看答案和解析>>
科目:初中数学 来源: 题型:
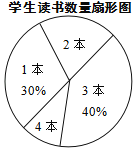
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )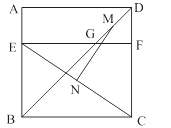
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:

请依据统计结果回答下列问题:
(1)本次调查中,一共调查了 位好友.
(2)已知A类好友人数是D类好友人数的5倍.
①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)设![]() 若
若![]() 求A-2B的值;
求A-2B的值;
(2)某公司有甲、乙两类经营收入,去年甲类收入是乙类收入的2倍,预计今年甲类年收入减少9%,乙类收入将增加19%。问今年该公司的年总收入比去年增加了吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究函数y=x+ ![]() 的图象与性质】
的图象与性质】
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中函数y=x+ ![]() 的图象大致是;
的图象大致是; 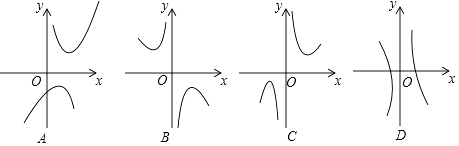
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
,求当x>0时,y的取值范围. 请将下列的求解过程补充完整.
解:∵x>0
∴y=x+ ![]() =(
=( ![]() )2+(
)2+( ![]() )2=(
)2=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0
)2≥0
∴y≥ .
(4)若函数y= ![]() ,则y的取值范围 .
,则y的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com