
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
【答案】(1)45, 35; (2)1个,2个; (3)答案见解析.
【解析】
(1)根据单价×数量=钱数求解即可;
(2)设甲居民购买了垃圾桶x个,塑料鞋架y个,根据一共买了8个家居用品和一共花了280元钱各列一个方程组成方程组求解即可;
(3)设甲居民购买了艺术饰品z个,垃圾桶w个,可得方程45z+15w=150,即w=10-3z,然后结合w,z是正整数讨论即可.
(1)a=90÷2=45,b=35×1=35;
(2)设甲居民购买了垃圾桶x个,塑料鞋架y个,
依题意,得![]() 解得
解得![]()
答:甲居民购买了垃圾桶1个,塑料鞋架2个.
(3)设甲居民购买了艺术饰品z个,垃圾桶w个依题意,得:
45z+15w=150,则w=10-3z.
因为z,w都是正整数,
所以当z=1时,w=7,
当z=2时,w=4,当z=3时,w=1,
故有3种购买方案:①购买艺术饰品1个,垃圾桶7个;②购买艺术饰品2个,垃圾桶4个;③购买艺术饰品3个,垃圾桶1个.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
材料一:分解因式是将一个多项式化为若干个整式积的形式的变形,“十字相乘法”可把某些二次三项式分解为两个一次式的乘积,具体做法如下:对关于![]() ,
,![]() 的二次三项式
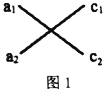
的二次三项式![]() ,如图1,将
,如图1,将![]() 项系数
项系数![]() ,作为第一列,
,作为第一列,![]() 项系数
项系数![]() ,作为第二列,若
,作为第二列,若![]() 恰好等于
恰好等于![]() 项的系数
项的系数![]() ,那么
,那么![]() 可直接分解因式为:
可直接分解因式为:![]()
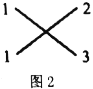
示例1:分解因式:![]()
解:如图2,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;
示例2:分解因式:![]() .
.
解:如图3,其中![]() ,
,![]() ,而
,而![]() ;
;
∴![]() ;
;

材料二:关于![]() ,
,![]() 的二次多项式
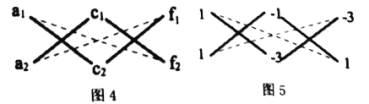
的二次多项式![]() 也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将
也可以用“十字相乘法”分解为两个一次式的乘积.如图4,将![]() 作为一列,
作为一列,![]() 作为第二列,
作为第二列,![]() 作为第三列,若
作为第三列,若![]() ,
,![]() ,
,![]() ,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:
,即第1、2列,第1、3列和第2、3列都满足十字相乘规则,则原式分解因式的结果为:![]() ;
;
示例3:分解因式:![]() .
.
解:如图5,其中![]() ,
,![]() ,
,![]() ;
;
满足![]() ,
,![]() ;
;
∴![]()
请根据上述材料,完成下列问题:
(1)分解因式:![]() ;
;![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 均为整数,且关于
均为整数,且关于![]() ,
,![]() 的二次多项式
的二次多项式![]() 可用“十字相乘法”分解为两个一次式的乘积,求出
可用“十字相乘法”分解为两个一次式的乘积,求出![]() 的值,并求出关于
的值,并求出关于![]() ,
,![]() 的方程
的方程![]() 的整数解.
的整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
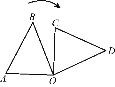
【题目】如图,△AOB绕点O按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?多少度?
(2)指出线段AB的对应线段,∠A,∠B的对应角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等问题.
例如:分解因式![]() ;求代数式
;求代数式![]() 的最小值,
的最小值,![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _______.
_______.
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
(3)利用配方法,尝试解方程![]() ,并求出
,并求出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
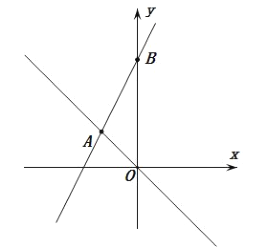
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)在平面直角坐标系中有一点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 满足的关系式是什么?
满足的关系式是什么?
(3)已知平行于![]() 轴且位于
轴且位于![]() 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() 且点
且点![]() 在点
在点![]() 的下方,点
的下方,点![]() 为
为![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
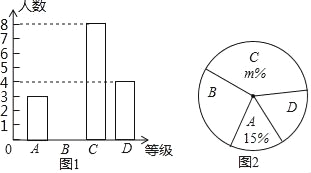
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为 ,表示“D等级”的扇形的圆心角为 度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:
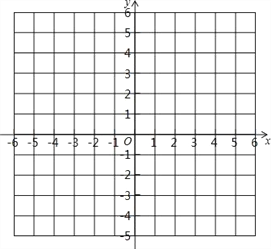
【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com