
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)在平面直角坐标系中有一点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 满足的关系式是什么?
满足的关系式是什么?
(3)已知平行于![]() 轴且位于
轴且位于![]() 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() 且点
且点![]() 在点
在点![]() 的下方,点
的下方,点![]() 为
为![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点![]() 的坐标.
的坐标.
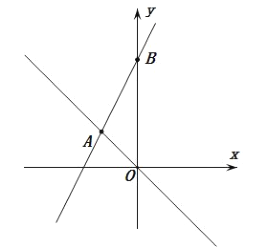
【答案】(1)![]() 的解析式为
的解析式为![]() ;(2) m+n=3或m+n=-3;(3)
;(2) m+n=3或m+n=-3;(3) ![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).
【解析】
(1)可得A(-1,1)B(0,3),设![]() 的解析式为
的解析式为![]() ,代入A(-1,1),可得
,代入A(-1,1),可得![]() 的解析式;
的解析式;
(2)①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]() ,
,![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P
B的解析式为:y=-x+3,即:n=-m+3,m+n=3,②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,,可得B点关于O点的对称点位
,,,可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,可得Q的值,
,可得Q的值,
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,可得Q的值.
,可得Q的值.
解:(1)由题可得: a=-1,b=3
则点A(-1,1)B(0,3)
设![]() 的解析式为
的解析式为![]() ,代入A(-1,1)得:1=-k+3,
,代入A(-1,1)得:1=-k+3,
解得:k=2,
![]()
![]() 的解析式为
的解析式为![]()
(2)![]() ,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
,则点P到AO的距离与点B到AO的距离相等,且点P位于h两侧;
①当点P在![]() 的右侧时,设点P为
的右侧时,设点P为![]() ,且
,且![]() B//
B//![]()
![]()
![]() B的解析式为:y=-x+3,即:n=-m+3,m+n=3
B的解析式为:y=-x+3,即:n=-m+3,m+n=3
②当点P![]() 在的左侧时,设点P为
在的左侧时,设点P为![]() ,,
,,
可得B点关于O点的对称点位![]() (0,-3)点在
(0,-3)点在![]() ;
;![]() 上,且
上,且![]()
![]() //
//![]() ,
,
![]()
![]()
![]() 的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
的解析式为:y=-x-3,即:n=-m-3,m+n=-3;
综合:m+n=3或m+n=-3;
(3)设动直线为x=t,由题可得-1<t<0,
则M(t,-t),N(t,2t+3),MN=3t+3,
当NM⊥NQ且NM=NQ时,Q(0,2t+3),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当MN⊥MQ且NM=MQ时,Q(0,-t),由3t+3=-t,t=-![]() ,此时
,此时![]() (0,
(0,![]() )
)
当QN⊥QM且QN=QM时,Q(0,![]() ),可得2t+3-(
),可得2t+3-(![]() )=-t,解得t=
)=-t,解得t=![]() ,此时
,此时![]() (0,
(0,![]() ),
),
综上![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ),
),![]() (0,
(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用A、B、C、D表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我校“书香校园”活动中,某数学小组为了解学生家庭藏书情况,随机抽取我校部分学生进行调查,并绘制成部分统计图如下表:
类别 | 家庭藏书情况统计表 | 学生人数 |
|
| 20 |
|
|
|
|
| 50 |
|
| 66 |
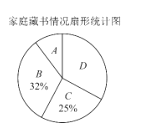
根据以上信息,解答下列问题:
(1)参加调查的学生人数为多少,a等于多少,本次调查结果的中位数在哪一类.
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为多少.
”对应扇形的圆心角为多少.
(3)若我校有4500名学生,请估计全校学生中藏书200本以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)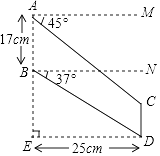
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:
第1个式子: ![]()
第2个式子: ![]()
第3个式子: ![]()
第4个式子: ![]()
![]()
(1)可猜想第7个等式为 .
(2)探索规律,若字母![]() 表示自然数,请写出第
表示自然数,请写出第![]() 个等式 .
个等式 .
(3)试证明你写出的等式的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com