
【题目】某商店决定购进A、B两种纪念品.若购进A种纪念品8件,B种纪念品3件,需要95元;若购进A种纪念品5件,B种纪念品6件,需要80元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于750元,但不超过764元,那么该商店共有几种进货方案?
(3)已知商家出售一件A种纪念品可获利a元,出售一件B种纪念品可获利(5﹣a)元,试问在(2)的条件下,商家采用哪种方案可获利最多?(商家出售的纪念品均不低于成本价)
【答案】(1)A、B两种纪念品的价格分别为10元和5元;(2)该商店共有3种进货方案(3)若![]() 时,购进52件A纪念品,48件B纪念品获利最大;若
时,购进52件A纪念品,48件B纪念品获利最大;若![]() 时,购进50件A纪念品,50件B纪念品获利最大;若
时,购进50件A纪念品,50件B纪念品获利最大;若![]() 时,此时三种进货方案获利相同.
时,此时三种进货方案获利相同.
【解析】
(1)设A种纪念品每件x元,B种纪念品每件y元,根据购进A种纪念品8件,B种纪念品3件,需要95元和购进A种纪念品5件,B种纪念品6件,需要80元,列出方程组,再进行求解即可;
(2)设商店最多可购进A纪念品m件,则购进B纪念品(100-m)件,根据购买这100件纪念品的资金不少于750元,但不超过764元,列出不等式组,再进行求解即可;
(3)将总利润y表示成所进A纪念品件数x的函数,分类讨论,根据函数的单调性判断那种方案利润最大.
解:(1)设A、B两种纪念品的价格分别为x元和y元,则
![]() ,解得
,解得![]() .
.
答:A、B两种纪念品的价格分别为10元和5元.
(2)设购买A种纪念品m件,则购买B种纪念品(100- m)件,则
750≤10m+5(100-m)≤764,
解得50≤m≤52.8,
∵m为正整数,
∴m=50,51,52,
即有三种方案.
第一种方案:购A种纪念品50件,B种纪念品50件;
第二种方案:购A种纪念品51件,B种纪念品49件;
第三种方案:购A种纪念品52件,B种纪念品48件;
(3)设商家购进x件A纪念品,所获利润为y,
则y=ax+(100-x)(5-a)=(2a-5)x+500-100a.
∵商家出售的纪念品均不低于成本,
![]() ,即0≤a≤5.
,即0≤a≤5.
①若2a-5>0即![]() 时,y=(2a-5)x+500-100a,y随x增大而增大.
时,y=(2a-5)x+500-100a,y随x增大而增大.
此时购进52件A纪念品,48件B纪念品获利最大.
②若2a-5<0,即![]() 时,y=(2a-5)x+500-100a,y随x增大而减小.
时,y=(2a-5)x+500-100a,y随x增大而减小.
此时购进50件A纪念品,50件B纪念品获利最大.
③若2a-5=0,即![]() 时,则y=250,为常数函数,
时,则y=250,为常数函数,
此时三种进货方案获利相同.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】在下列说法中:①过一点有且只有一条直线与已知直线平行;②-0.9是0.81的平方根;③若在平面直角坐标系中直线![]() 垂直于
垂直于![]() 轴,则直线
轴,则直线![]() 上所有的点的横坐标相同;④
上所有的点的横坐标相同;④![]() 是一个负数;⑤0的相反数和倒数都是0;⑥
是一个负数;⑤0的相反数和倒数都是0;⑥![]() ;⑦
;⑦![]() ;⑧全体有理数和数轴上的点一一对应.以上真命题的序号是__________.
;⑧全体有理数和数轴上的点一一对应.以上真命题的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
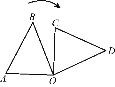
【题目】如图,△AOB绕点O按顺时针方向旋转得到△COD,当OA⊥OC时,在这个旋转过程中:
(1)旋转中心是什么?旋转角是什么?多少度?
(2)指出线段AB的对应线段,∠A,∠B的对应角.
查看答案和解析>>
科目:初中数学 来源: 题型:
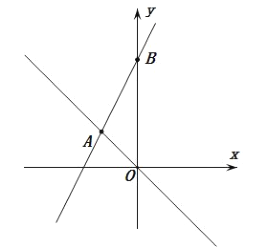
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)在平面直角坐标系中有一点![]() ,若
,若![]() ,则
,则![]() 与
与![]() 满足的关系式是什么?
满足的关系式是什么?
(3)已知平行于![]() 轴且位于
轴且位于![]() 轴左侧有一动直线,分别与
轴左侧有一动直线,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() 且点
且点![]() 在点
在点![]() 的下方,点
的下方,点![]() 为
为![]() 轴上一动点,且
轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点
为等腰直角三角形,请直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
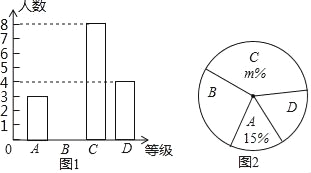
【题目】为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成图1的条形统计图和图2扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)求参加比赛的学生共有多少名?并补全图1的条形统计图.
(2)在图2扇形统计图中,m的值为 ,表示“D等级”的扇形的圆心角为 度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图1中阴影部分的面积.

方法①: ;
方法②: ;
(2)根据(1)写出一个等式: ;
(3)若x+y=8,xy=3.75,利用(2)中的结论,求x,y;
(4)有许多代数恒等式可以用图形的面积来表示.如图2,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(2m+n)(m+2n)=2m2+5mn+2n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3, 求证:AD平分∠BAC.
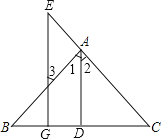
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°( )
∴∠ADC=∠EGC(等量代换)
∴AD∥EG( )
∴∠1=∠3( )
∠2=∠E( )
又∵∠E=∠3( 已知) ∴∠1=∠2( )
∴AD平分∠BAC( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°, 试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式, 将答案按序号填在答题卷的对应位置内)
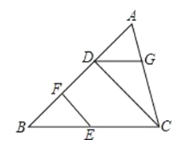
证明:∵CD⊥AB,EF⊥AB( ① )
∴∠BFE=∠BDC=90°( ② )
∴EF∥CD( ③ )
∴∠BEF= ④ ( ⑤ )
又∵∠B+∠BDG=180°( ⑥ )
∴BC∥DG( ⑦ )
∴∠CDG= ⑧ ( ⑨ )
∴∠CDG=∠BEF( ⑩ )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com